
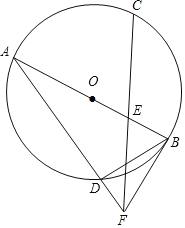
【题目】如图,AB是⊙O的直径,![]() ,E是OB的中点,连接CE并延长到点F,使EF=CE.连接AF交⊙O于点D,连接BD,BF.
,E是OB的中点,连接CE并延长到点F,使EF=CE.连接AF交⊙O于点D,连接BD,BF.
(1)求证:直线BF是⊙O的切线;
(2)若OB=2,求BD的长.
【答案】(1)证明见解析;(2)BD=![]() .
.
【解析】(1)连接OC,由已知可得∠BOC=90°,根据SAS证明△OCE≌△BFE,根据全等三角形的对应角相等可得∠OBF=∠COE=90°,继而可证明直线BF是⊙O的切线;
(2),由(1)的全等可知BF=OC=2,利用勾股定理求出AF的长,然后由S△ABF=![]() ,即可求出BD=
,即可求出BD=![]() .
.
(1)连接OC,
∵AB是⊙O的直径,![]() ,∴∠BOC=90°,
,∴∠BOC=90°,
∵E是OB的中点,∴OE=BE,
在△OCE和△BFE中,
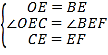 ,
,
∴△OCE≌△BFE(SAS),
∴∠OBF=∠COE=90°,
∴直线BF是⊙O的切线;
(2)∵OB=OC=2,由(1)得:△OCE≌△BFE,
∴BF=OC=2,
∴AF=![]() ,
,
∴S△ABF=![]() ,
,
即4×2=2![]() BD,
BD,
∴BD=![]() .
.


科目:初中数学 来源: 题型:
【题目】某工厂准备购买A、B两种零件,已知A种零件的单价比B种零件的单价多30元,而用900元购买A种零件的数量和用600元购买B种零件的数量相等.
(1)求A、B两种零件的单价;
(2)根据需要,工厂准备购买A、B两种零件共200件,工厂购买两种零件的总费用不超过14700元,求工厂最多购买A种零件多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
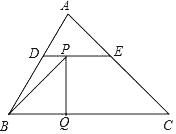
【题目】如图,在△ABC中,∠ABC=60°,∠C=45°,点D,E分别为边AB,AC上的点,且DE∥BC,BD=DE=2,CE=![]() ,BC=
,BC=![]() .动点P从点B出发,以每秒1个单位长度的速度沿B→D→E→C匀速运动,运动到点C时停止.过点P作PQ⊥BC于点Q,设△BPQ的面积为S,点P的运动时间为t,则S关于t的函数图象大致为( )
.动点P从点B出发,以每秒1个单位长度的速度沿B→D→E→C匀速运动,运动到点C时停止.过点P作PQ⊥BC于点Q,设△BPQ的面积为S,点P的运动时间为t,则S关于t的函数图象大致为( )
A. 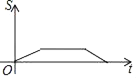 B.
B. 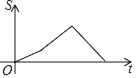
C. 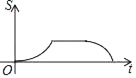 D.
D. 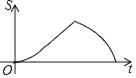
查看答案和解析>>
科目:初中数学 来源: 题型:
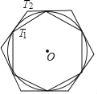
【题目】T1、T2分别为⊙O的内接正六边形和外切正六边形.设T1的半径r,T1、T2的边长分别为a、b,T1、T2的面积分别为S1、S2.下列结论:①r:a=1:1;②r:b=![]() ;③a:b=1:
;③a:b=1:![]() ;④S1:S2=3:4.其中正确的有_____.(填序号)
;④S1:S2=3:4.其中正确的有_____.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
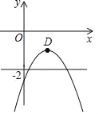
【题目】如图,在直角坐标系xOy中,若抛物线l:y=﹣![]() x2+bx+c(b,c为常数)的顶点D位于直线y=﹣2与x轴之间的区域(不包括直线y=﹣2和x轴),则l与直线y=﹣1交点的个数是( )
x2+bx+c(b,c为常数)的顶点D位于直线y=﹣2与x轴之间的区域(不包括直线y=﹣2和x轴),则l与直线y=﹣1交点的个数是( )
A. 0个B. 1个或2个
C. 0个、1个或2个D. 只有1个
查看答案和解析>>
科目:初中数学 来源: 题型:
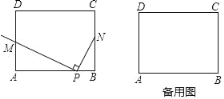
【题目】如图,在矩形ABCD中,AB=4,AD=3,点N为BC边上的一点,且BN=n(n>0),动点P从点A出发,以每秒1个单位长的速度沿AB边向点B运动,连接NP,作射线PM⊥NP交AD于点M,设点P运动的时间是t秒(t>0).
(1)当点M与点A重合时,t等于多少秒,当点M与点D重合时,n等于多少(用含字母t的代数式表示)
(2)若n=2,则
①在点P运动过程中,点M是否可以到达线段AD的延长线上?通过计算说明理由;
②连接ND,当t为何值时,ND∥PM?
(3)过点N作NK∥AB,交AD于点K,若在点P运动过程中,点K与点M不会重合,直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
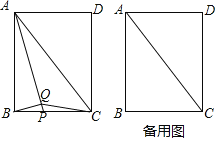
【题目】如图,在矩形ABCD中,AC为对角线,点P为BC边上一动点,连接AP,过点B作BQ⊥AP,垂足为Q,连接CQ.
⑴证明:△ABP∽△BQP;
⑵当点P为BC的中点时,若∠BAC=37°,求∠CQP的度数;
⑶当点P运动到与点C重合时,延长BQ交CD于点F,若AQ=AD,则![]() 等于多少.
等于多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B为定点,定直线l//AB,P是l上一动点.点M,N分别为PA,PB的中点,对于下列各值:
①线段MN的长;
②△PAB的周长;
③△PMN的面积;
④直线MN,AB之间的距离;
⑤∠APB的大小.
其中会随点P的移动而变化的是( )

A. ②③ B. ②⑤ C. ①③④ D. ④⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com