
ЁОЬтФПЁПЯШдФЖСРэНтЯТУцЕФР§ЬтЃЌдйАДвЊЧѓНтД№ЯТСаЮЪЬтЃК
НтЗНГЬЃЈ![]() ЃЉ2Љ6ЃЈ
ЃЉ2Љ6ЃЈ![]() ЃЉ+5=0
ЃЉ+5=0
НтЃКСю![]() =yЃЌДњШыдЗНГЬКѓЃЌЕУЃК
=yЃЌДњШыдЗНГЬКѓЃЌЕУЃК
y2Љ6y+5=0
ЃЈyЉ5ЃЉЃЈyЉ1ЃЉ=0
НтЕУЃКy1=5 y2=1
Ёп![]() =y
=y
Ёр![]() =5Лђ
=5Лђ![]() =1
=1
ЂйЕБ![]() =1ЪБЃЌЗНГЬПЩБфЮЊЃК
=1ЪБЃЌЗНГЬПЩБфЮЊЃК
x=5ЃЈxЉ1ЃЉ
НтЕУx=![]()
ЂкЕБ![]() =1ЪБЃЌЗНГЬПЩБфЮЊЃК
=1ЪБЃЌЗНГЬПЩБфЮЊЃК
x=xЉ1
ДЫЪБЃЌЗНГЬЮоНт
МьбщЃКНЋx=![]() ДњШыдЗНГЬЃЌ
ДњШыдЗНГЬЃЌ
зюМђЙЋЗжФИВЛЮЊ0ЃЌЧвЗНГЬзѓБп=гвУц
Ёрx=![]() ЪЧдЗНГЬЕФИљ
ЪЧдЗНГЬЕФИљ
злЩЯЫљЪіЃКдЗНГЬЕФИљЮЊЃКx=![]()
ИљОнвдЩЯВФСЯЃЌНтЙигкxЕФЗНГЬx2+![]() +x+
+x+![]() =0ЃЎ
=0ЃЎ
ЁОД№АИЁПx=Љ1ЃЎ
ЁОНтЮіЁП
ЯШБфаЮЃЌЩшx+![]() =aЃЌдђдЗНГЬЛЏЮЊa2+aЉ2=0ЃЌЧѓГіaЕФжЕЃЌдйДњШыЧѓГіxЕФжЕЃЌзюКѓНјааМьбщМДПЩЃЎ
=aЃЌдђдЗНГЬЛЏЮЊa2+aЉ2=0ЃЌЧѓГіaЕФжЕЃЌдйДњШыЧѓГіxЕФжЕЃЌзюКѓНјааМьбщМДПЩЃЎ
x2+![]() +x+
+x+![]() =0ЃЌЃЈx+
=0ЃЌЃЈx+![]() ЃЉ2+x+
ЃЉ2+x+![]() Љ2=0ЃЌЩшx+
Љ2=0ЃЌЩшx+![]() =aЃЌдђдЗНГЬЛЏЮЊЃКa2+aЉ2=0
=aЃЌдђдЗНГЬЛЏЮЊЃКa2+aЉ2=0
НтЕУЃКa=Љ2Лђ1ЃЎ
ЕБa=Љ2ЪБЃЌx+![]() =Љ2ЃЌx2+2x+1=0ЃЌНтЕУЃКx=Љ1ЃЛ
=Љ2ЃЌx2+2x+1=0ЃЌНтЕУЃКx=Љ1ЃЛ
ЕБa=1ЪБЃЌx+![]() =1ЃЌx2Љx+1=0ЃЌДЫЗНГЬЮоНтЃЎ
=1ЃЌx2Љx+1=0ЃЌДЫЗНГЬЮоНтЃЎ
ОМьбщx=Љ1ЪЧдЗНГЬЕФНтЃЌЫљвддЗНГЬЕФНтЮЊx=Љ1ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁОЮЪЬтЧщОГЁП
ПЮЭтаЫШЄаЁзщЛюЖЏЪБЃЌРЯЪІЬсГіСЫШчЯТЮЪЬтЃК
ШчЭМЂйЃЌЁїABCжаЃЌШєABЃН12ЃЌACЃН8ЃЌЧѓBCБпЩЯЕФжаЯпADЕФШЁжЕЗЖЮЇЃЎ
аЁУїдкзщФкОЙ§КЯзїНЛСїЃЌЕУЕНСЫШчЯТЕФНтОіЗНЗЈЃКбгГЄADжСЕуEЃЌЪЙDEЃНADЃЌСЌНгBEЃЎЧыИљОнаЁУїЕФЗНЗЈЫМПМЃК
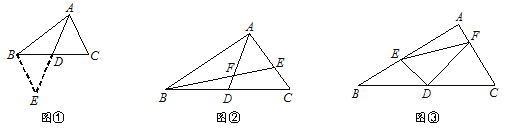
ЃЈ1ЃЉгЩвбжЊКЭзїЭМФмЕУЕНЁїADCЁеЁїEDBЃЌвРОнЪЧ ЃЎ
AЃЎSSS BЃЎSAS CЃЎAAS DЃЎHL
ЃЈ2ЃЉгЩЁАШ§НЧаЮЕФШ§БпЙиЯЕЁБПЩЧѓЕУADЕФШЁжЕЗЖЮЇЪЧ ЃЎ
НтКѓЗДЫМЃКЬтФПжаГіЯжЁАжаЕуЁБЁЂЁАжаЯпЁБЕШЬѕМўЃЌПЩПМТЧбгГЄжаЯпЙЙдьШЋЕШШ§НЧаЮЃЌАбЗжЩЂЕФвбжЊЬѕМўКЭЫљЧѓжЄЕФНсТлМЏжаЕНЭЌвЛИіШ§НЧаЮжЎжаЃЎ
ЁОГѕВНдЫгУЁП
ШчЭМЂкЃЌADЪЧЁїABCЕФжаЯпЃЌBEНЛACгкEЃЌНЛADгкFЃЌЧвAEЃНEFЃЎШєEFЃН3ЃЌECЃН2ЃЌЧѓЯпЖЮBFЕФГЄЃЎ
ЁОСщЛюдЫгУЁП
ШчЭМЂлЃЌдкЁїABCжаЃЌ ЁЯAЃН90ЁуЃЌDЮЊBCжаЕуЃЌ DEЁЭDFЃЌDEНЛABгкЕуEЃЌDFНЛACгкЕуFЃЌСЌНгEFЃЎЪдВТЯыЯпЖЮBEЁЂCFЁЂEFШ§епжЎМфЕФЕШСПЙиЯЕЃЌВЂжЄУїФуЕФНсТлЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌЕуDдкЁїABCЕФБпBCЩЯЃЌAB=AC=CDЃЌAD=BDЃЌЧѓЁїABCИїФкНЧЕФЖШЪ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЁїABCЃЌABЁЂACЕФДЙжБЦНЗжЯпЕФНЛЕуDЧЁКУТфдкBCБпЩЯ
(1)ХаЖЯЁїABCЕФаЮзД
(2)ШєЕуAдкЯпЖЮDCЕФДЙжБЦНЗжЯпЩЯЃЌЧѓ![]() ЕФжЕ
ЕФжЕ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
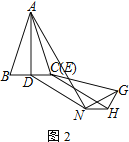
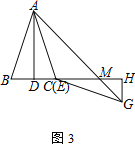
ЁОЬтФПЁПШчЭМ1ЃЌABЃНACЃЌEFЃНEGЃЌЁїABCЁеЁїEFGЃЌADЁЭBCгкЕуDЃЌEHЁЭFGгкЕуH
(1) жБНгаДГіADЁЂEHЕФЪ§СПЙиЯЕЃК___________________
(2) НЋЁїEFGбиEHМєПЊЃЌШУЕуEКЭЕуCжиКЯ
Ђй АДЭМ2ЗХжУЁїEHGЃЌНЋЯпЖЮCDбиEHЦНвЦжСHNЃЌСЌНгANЁЂGNЃЌЧѓжЄЃКANЁЭGN
Ђк АДЭМ3ЗХжУЁїEHGЃЌBЁЂCЃЈEЃЉЁЂHШ§ЕуЙВЯпЃЌСЌНгAGНЛEHгкЕуMЃЎШєBDЃН1ЃЌADЃН3ЃЌЧѓCMЕФГЄЖШ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯC=90ЁуЃЌAB=10cmЃЌBC=6cmЃЌШєЖЏЕуPДгЕуCПЊЪМГіЗЂЃЌАДCЁњAЁњBЁњCЕФТЗОЖдЫЖЏЃЌЧвЫйЖШЮЊУПУы2cmЃЌЩшГіЗЂЕФЪБМфЮЊtУыЃЎ
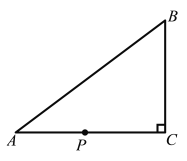
ЃЈ1ЃЉЬюПеЃКAC= cmЃЛ
ЃЈ2ЃЉШєЕуPЧЁКУдкЁЯABCЕФНЧЦНЗжЯпЩЯЃЌЧѓtЕФжЕЃЛ
ЃЈ3ЃЉЕБtЮЊКЮжЕЪБЃЌЁїBPCЮЊЕШбќШ§НЧаЮ?
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌШ§НЧаЮABCШ§ИіЖЅЕуAЃЌBЃЌCЕФзјБъЗжБ№ЮЊAЃЈ1ЃЌ2ЃЉЃЌBЃЈ4ЃЌ3ЃЉЃЌCЃЈ3ЃЌ1ЃЉ.АбШ§НЧаЮA1B1C1ЯђгвЦНвЦ4ИіЕЅЮЛГЄЖШЃЌдйЯђЯТЦНвЦ3ИіЕЅЮЛГЄЖШЃЌЧЁКУЕУЕНШ§НЧаЮABCЃЌЪдаДГіШ§НЧаЮA1B1C1Ш§ИіЖЅЕуЕФзјБъЃЌзїГіШ§НЧаЮABCЯђгвЦНвЦ1ИіЕЅЮЛЯђЯТЦНвЦ2ИіЕЅЮЛЕФЭМаЮ.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌАДвдЯТВНжшзїЭМЃК
ЂйвдBЮЊдВаФЃЌШЮвтГЄЮЊАыОЖзїЛЁЃЌНЛABгкDЃЌНЛBCгкEЃЛ
ЂкЗжБ№вдDЃЌEЮЊдВаФЃЌвдДѓгк![]() DEЕФЭЌбљГЄЮЊАыОЖзїЛЁЃЌСНЛЁНЛгкЕуFЃЛ
DEЕФЭЌбљГЄЮЊАыОЖзїЛЁЃЌСНЛЁНЛгкЕуFЃЛ
ЂлзїЩфЯпBFНЛACгкG.
ШчЙћBG=CGЃЌЁЯA=60ЁуЃЌФЧУДЁЯACBЕФЖШЪ§ЮЊ____________ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
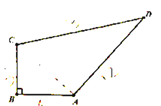
ЁОЬтФПЁПШчЭМЃЌаЁУїЕФАжАждкгуГиБпПЊСЫвЛПщЫФБпаЮЭСЕижжСЫвЛаЉЪпВЫЃЌАжАжШУаЁУїМЦЫуетПщЭСЕиЕФУцЛ§ЃЌвдБуЙРЫуВњжЕЃЌаЁУїВтЕУAB=4m,BC=3m,CD=13m.DA=12m.гжвбжЊЁЯB=90ЁуЃЌУПЦНЗНУзЭЖШызЪН№80дЊЃЌдЄМЦЯњЪлКѓВњжЕУПЦНЗНУз480дЊЃЌЪдЧѓГіетПщЭСЕиФмВњЩњЖрЩйРћШѓ?
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com