
 如图,在平面直角坐标系中,⊙P的半径为4,圆心P坐标是(4,a)(a>4),函数y=x的图象被⊙P截得的弦AB的长为4$\sqrt{3}$,则a的值是4+2$\sqrt{2}$.
如图,在平面直角坐标系中,⊙P的半径为4,圆心P坐标是(4,a)(a>4),函数y=x的图象被⊙P截得的弦AB的长为4$\sqrt{3}$,则a的值是4+2$\sqrt{2}$. 分析 PC⊥x轴于C,交AB于D,作PE⊥AB于E,连结PB,由于OC=4,PC=a,易得D点坐标为(4,4),则△OCD为等腰直角三角形,△PED也为等腰直角三角形.由PE⊥AB,根据垂径定理得AE=BE=$\frac{1}{2}$AB=2$\sqrt{3}$,在Rt△PBE中,利用勾股定理可计算出PE=2,则PD=$\sqrt{2}$PE=2$\sqrt{2}$,所以a=4+2$\sqrt{2}$.
解答 解:作PC⊥x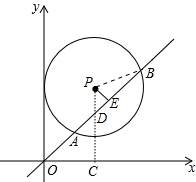 轴于C,交AB于D,作PE⊥AB于E,连结PB,如图,
轴于C,交AB于D,作PE⊥AB于E,连结PB,如图,
∵⊙P的圆心坐标是(4,a),
∴OC=4,PC=a,
把x=4代入y=x得y=4,
∴D点坐标为(4,4),
∴CD=4,
∴△OCD为等腰直角三角形,
∴△PED也为等腰直角三角形,
∵PE⊥AB,
∴AE=BE=$\frac{1}{2}$AB=$\frac{1}{2}$×4$\sqrt{3}$=2$\sqrt{3}$,
在Rt△PBE中,PB=4,
∴PE=$\sqrt{{4}^{2}-(2\sqrt{3})^{2}}$=2,
∴PD=$\sqrt{2}$PE=2$\sqrt{2}$,
∴a=4+2$\sqrt{2}$.
故答案为:4+2$\sqrt{2}$.
点评 本题主要考查了一次函数的综合应用,涉及圆的性质、垂径定理、等腰直角三角形的性质、勾股定理等知识点.作出P到x轴的距离、求得D点的坐标是解题的关键,本题所考查知识较基础,难度不大.


科目:初中数学 来源: 题型:选择题
| A. | 4x2-4x+1=(1-2x)2 | B. | x2+2x-1=(x-1)2 | C. | -x2+(-2)2=(x-2)(x+2) | D. | x2-4x=2(x+2)(x-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,C、D是以AB为直径的圆O上的两个动点(点C、D不与A、B重合),在运动过程中弦CD始终保持不变,M是弦CD的中点,过点C作CP⊥AB于点P.若CD=3,AB=5,PM=x,则x的最大值是( )
如图,C、D是以AB为直径的圆O上的两个动点(点C、D不与A、B重合),在运动过程中弦CD始终保持不变,M是弦CD的中点,过点C作CP⊥AB于点P.若CD=3,AB=5,PM=x,则x的最大值是( )| A. | 3 | B. | $\sqrt{5}$ | C. | 2.5 | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,O是正方形ABCD的中心,M是ABCD内一点,∠DMC=90°,将△DMC绕O点旋转180°后得到△NAB,若MD=3,CM=4,则MN的长为$\sqrt{2}$.
如图,O是正方形ABCD的中心,M是ABCD内一点,∠DMC=90°,将△DMC绕O点旋转180°后得到△NAB,若MD=3,CM=4,则MN的长为$\sqrt{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com