Question

10．对任意x，y∈R，代数式M=$\sqrt{2{x}^{2}-6x+5}$+$\sqrt{{y}^{2}-4y+5}$+$\sqrt{2{x}^{2}-2xy+{y}^{2}}$的最小值为$\sqrt{10}$．

Answer 1

分析 可将不熟悉的“求三个二次根式和的最小值”的问题转化为熟悉的“求三条线段和的最小值“的问题．若A的坐标为（1，2），B的坐标为（x，x），C的坐标为（y，0），D的坐标为（2，1），则根据勾股定理可得AB=$\sqrt{2{x}^{2}-6x+5}$，BC=$\sqrt{2{x}^{2}-2xy+{y}^{2}}$，CD=$\sqrt{{y}^{2}-4y+5}$，从而得到原式=AB+BC+CD，只需求出AB+BC+CD的最小值就可解决问题．

解答 解：如图，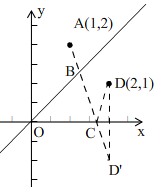
∵M=$\sqrt{2{x}^{2}-6x+5}$+$\sqrt{{y}^{2}-4y+5}$+$\sqrt{2{x}^{2}-2xy+{y}^{2}}$
=$\sqrt{（x-1）^{2}+（x-2）^{2}}$+$\sqrt{（y-2）^{2}+（0-1）^{2}}$+$\sqrt{（x-y）^{2}+（x-0）^{2}}$，
∴$\sqrt{（x-1）^{2}+（x-2）^{2}}$是点A（1，2）与点B（x，x）的距离，
$\sqrt{（y-2）^{2}+（0-1）^{2}}$是点C（y，0）与点D（2，1）的距离，
$\sqrt{（x-y）^{2}+（x-0）^{2}}$是点B（x，x）与C（y，0）的距离；
∴M=AB+BC+CD．
∵点B（x，x）在直线y=x上，点C（y，0）在x轴上，
作点D（2，1）关于x轴的对称点D'（2，-1），
根据两点之间线段最短可得：
当A、B、C、D'在同一条直线上时，AB+BC+CD=AB+BC+CD'最短，此时AB+BC+CD'的最小值等于AC+CD=AD'．
∵A（1，2），D'（2，-1），
∴AD'=$\sqrt{（1-2）^{2}+（2+1）^{2}}$=$\sqrt{10}$，
∴M=$\sqrt{2{x}^{2}-6x+5}$+$\sqrt{{y}^{2}-4y+5}$+$\sqrt{2{x}^{2}-2xy+{y}^{2}}$的最小值为$\sqrt{10}$，
故答案为：$\sqrt{10}$．

点评 本题主要考查了用待定系数法求一次函数的解析式、线段的垂直平分线的性质、勾股定理、两点之间线段最短等知识，考查了创造性思维和数形结合的思想，而把问题转化为求线段和的最小值是解决本题的关键．