
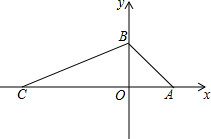
 如图,在平面直角坐标系中,O为坐标原点,直线y=-x+4与x轴交于点A,与y轴交于点B,点C在x轴负半轴上,S△ABC=28.点P是线段CA上一动点.
如图,在平面直角坐标系中,O为坐标原点,直线y=-x+4与x轴交于点A,与y轴交于点B,点C在x轴负半轴上,S△ABC=28.点P是线段CA上一动点.分析 (1)首先分别求出点A、B的坐标各是多少;然后根据S△ABC=28,求出点C的坐标;最后应用待定系数法,求出直线CB的解析式即可.
(2)首先连接EG并延长交CF的延长线于点Q,根据AE⊥EF,MG⊥EF,CQ⊥EF,判断出AE∥MG∥CQ;然后判断出△EMG∽△EFQ,推得EG=QG,再判断出△AEG∽△CQG,推得AG=CG;最后求出OG的长度,在Rt△OBG中,根据勾股定理,求出BG的长是多少即可.
(3)在平面内存在点R,使以点O,B,H,R为顶点的四边形是菱形.首先根据题意,分四种情况:①点R在第二象限;②点R在第三象限;③点R在第一象限,且HR∥OB;④点R在第一象限,且HB∥OR;然后根据菱形的性质分类讨论,求出点R的坐标是多少即可.
解答 解:(1)∵直线y=-x+4与x轴交于点A,与y轴交于点B,
∴A(4,0),B(0,4),
∵S△ABC=28,
∴S△ABC=$\frac{1}{2}AC•OB$=$\frac{1}{2}AC×4$=28,
∴AC=14,OC=10,
∴C(-10,0),
设直线CB的解析式是y=kx+b,
则$\left\{\begin{array}{l}{-10k+b=0}\\{b=4}\end{array}\right.$
解得$\left\{\begin{array}{l}{k=\frac{2}{5}}\\{b=4}\end{array}\right.$
∴直线CB的解析式是y=$\frac{2}{5}$x+4.
(2)如图1,连接EG并延长交CF的延长线于点Q,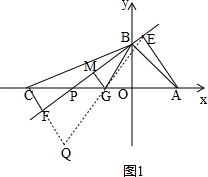 ,
,
∵AE⊥EF,MG⊥EF,CQ⊥EF,
∴AE∥MG∥CQ,
∴△EMG∽△EFQ,
∴$\frac{EG}{EQ}=\frac{EM}{EF}=\frac{1}{2}$,
∴EG=QG,
∵AE∥CQ,
∴△AEG∽△CQG,
∴$\frac{AG}{CG}=\frac{EG}{QG}$=1,
∴AG=CG,
∴AG=$\frac{1}{2}$AC=$\frac{1}{2}×14=7$,
∴OG=AG-AO=7-4=3,
在Rt△OBG中,
BG=$\sqrt{{OB}^{2}{+OG}^{2}}=\sqrt{{4}^{2}{+3}^{2}}=5$.
(3)在平面内存在点R,使以点O,B,H,R为顶点的四边形是菱形.
①如图2,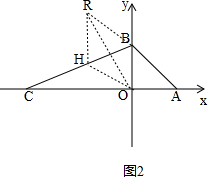 ,
,
∵四边形OBRH是菱形,
∴HR∥OB,HB⊥OR,
∴设H(a,$\frac{2}{5}$a+4),R(a,$\frac{2}{5}$b),
∵HR=OB,
∴-$\frac{5}{2}a$-($\frac{2}{5}$a+4)=4,
解得a=-$\frac{80}{29}$,
∴-$\frac{5}{2}$a=-$\frac{5}{2}$×$(-\frac{80}{29})$=$\frac{200}{29}$,
∴点R的坐标是(-$\frac{80}{29}$,$\frac{200}{29}$).
②如图3,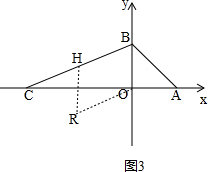 ,
,
∵四边形OBHR是菱形,
∴HR∥OB,HB∥OR,
∴设H(b,$\frac{2}{5}$b+4),R(b,$\frac{2}{5}b$),
∵OR=OB,
∴$\sqrt{{b}^{2}{+(\frac{2}{5}b)}^{2}}$=4,
解得b=-$\frac{20}{29}\sqrt{29}$,或b=$\frac{20}{29}\sqrt{29}$(舍去),
∴$\frac{2}{5}$a=$\frac{2}{5}$×(-$\frac{20}{29}\sqrt{29}$)=-$\frac{8}{29}\sqrt{29}$,
∴点R的坐标是(-$\frac{20}{29}\sqrt{29}$,-$\frac{8}{29}\sqrt{29}$).
③如图4,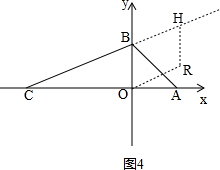 ,
,
∵四边OBHR是菱形,
∴HR∥OB,HB∥OR,
∴设H(c,$\frac{2}{5}$c+4),R(c,$\frac{2}{5}$c),
∵OR=OB,
∴$\sqrt{{c}^{2}{+(\frac{2}{5}c)}^{2}}$=4,
解得c=$\frac{20}{29}\sqrt{29}$,或c=-$\frac{20}{29}\sqrt{29}$(舍去),
∴$\frac{2}{5}$a=$\frac{2}{5}$×($\frac{20}{29}\sqrt{29}$)=$\frac{8}{29}\sqrt{29}$,
∴点R的坐标是($\frac{20}{29}\sqrt{29}$,$\frac{8}{29}\sqrt{29}$).
④如图5,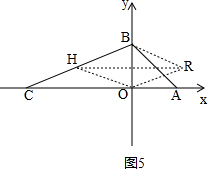 ,
,
∵四边形OHBR是菱形,
∴HB∥OR,HR⊥OB,
∵O(0,0)、B(0,4),
∴点H、R的纵坐标都是2,
∴设H(d,2),R(-d,2),
∵$\frac{2}{5}d+4$=2,
∴d=-5,
∴点R的坐标是(5,2).
综上,可得
在平面内存在点R,使以点O,B,H,R为顶点的四边形是菱形,
点R的坐标是(-$\frac{80}{29}$,$\frac{200}{29}$)、(-$\frac{20}{29}\sqrt{29}$,-$\frac{8}{29}\sqrt{29}$)、($\frac{20}{29}\sqrt{29}$,$\frac{8}{29}\sqrt{29}$)、(5,2).
点评 (1)此题主要考查了一次函数综合题,考查了分析推理能力,考查了分类讨论思想的应用,考查了数形结合思想的应用,考查了从已知函数图象中获取信息,并能利用获取的信息解答相应的问题的能力.
(2)此题还考查了菱形的性质和应用,要熟练掌握,解答此题的关键是要明确:①菱形具有平行四边形的一切性质;②菱形的四条边都相等; ③菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;④菱形是轴对称图形,它有2条对称轴,分别是两条对角线所在直线.
(3)此题还考查了相似三角形的性质和应用,以及待定系数法求直线解析式的方法,要熟练掌握.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
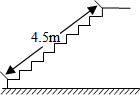 某中学要修建一座图书楼,为改善安全性能,把楼梯的倾斜角由原来设计的45°改为30°.已知原来设计的楼梯长为4.5m,在楼梯高度不变的情况下,调整后的楼梯多占地面$\frac{9\sqrt{6}-9\sqrt{2}}{4}$m.
某中学要修建一座图书楼,为改善安全性能,把楼梯的倾斜角由原来设计的45°改为30°.已知原来设计的楼梯长为4.5m,在楼梯高度不变的情况下,调整后的楼梯多占地面$\frac{9\sqrt{6}-9\sqrt{2}}{4}$m.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
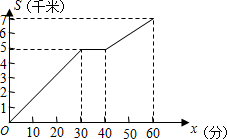 一名学生骑自行车沿笔直的公路出行,这名同学离开起点的距离y(单位:千米)与行驶的时间x(单位:分)图象如图所示,则下面的结论中正确的是( )
一名学生骑自行车沿笔直的公路出行,这名同学离开起点的距离y(单位:千米)与行驶的时间x(单位:分)图象如图所示,则下面的结论中正确的是( )| A. | 整个过程的平均速度是$\frac{7}{60}$千米/时 | B. | 该同学途中停了10分钟 | ||
| C. | 前20分钟的速度比后20分钟慢 | D. | 从起点到终点共用了50分钟 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
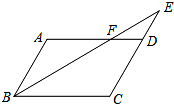 如图,在平行四边形ABCD中,点E是CD延长线上一点,BE与AD交于点F,若CD=2DE,且△DEF的面积为3,则三角形ABF的面积为( )
如图,在平行四边形ABCD中,点E是CD延长线上一点,BE与AD交于点F,若CD=2DE,且△DEF的面积为3,则三角形ABF的面积为( )| A. | 6 | B. | 8 | C. | 9 | D. | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
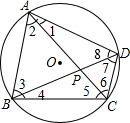 如图,圆内接四边形ABCD的对角线AC、BD把它的4个内角分成8个角,AC、BD相交于点P.
如图,圆内接四边形ABCD的对角线AC、BD把它的4个内角分成8个角,AC、BD相交于点P.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com