
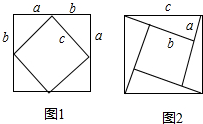
 勾股定理被誉为千古第一定理长期以来人们对他进行了大量的研究找到了数百种不同的验证方法这些方法不但验证了勾股定理而且丰富了研究数学问题的方法和手段促进了数学的发展请同学们利用图一图二分别证明勾股定理.
勾股定理被誉为千古第一定理长期以来人们对他进行了大量的研究找到了数百种不同的验证方法这些方法不但验证了勾股定理而且丰富了研究数学问题的方法和手段促进了数学的发展请同学们利用图一图二分别证明勾股定理. 分析 图中的大正方形的面积=小正方形的面积+4个小直角三角形的面积.利用正方形的面积公式和直角三角形的面积公式进行解答即可.
解答 证明:如图①,(a+b)2=4×$\frac{1}{2}$ab+c2,
a2+2ab+b2=2ab+c2,
a2+b2=c2.
即直角三角形的两直角边平方和等于斜边的平方;
如图②,c2=(b-a)2+4×$\frac{1}{2}$ab,
c2=b2-2ab+b2+2ab,
c2=a2+b2,即a2+b2=c2.
所以,直角三角形的两直角边平方和等于斜边的平方.
点评 本题考查了勾股定理的证明.证明勾股定理时,用几个全等的直角三角形拼成一个规则的图形,然后利用大图形的面积等于几个小图形的面积和化简整理得到勾股定理.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M在线段OA和射线AC上运动.
如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M在线段OA和射线AC上运动.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,∠B=90°,点M在AB上,AM=BC,作正方形CMDE,连接AD.
如图,△ABC中,∠B=90°,点M在AB上,AM=BC,作正方形CMDE,连接AD.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AE=CF,∠AFD=∠CEB,添加下列一个条件后,不能判定△ADF≌△CBE的是( )
如图,AE=CF,∠AFD=∠CEB,添加下列一个条件后,不能判定△ADF≌△CBE的是( )| A. | ∠A=∠C | B. | BE=DF | C. | AD∥BC | D. | AD=CB |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m>-1 | B. | m<-1 | C. | m<0 | D. | m<1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com