
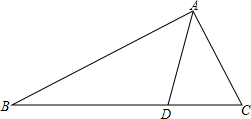
 如图,在△ABC中,AD平分∠BAC,∠C=2∠B,
如图,在△ABC中,AD平分∠BAC,∠C=2∠B,分析 在AB上取点E,使得AE=AC,则可证得△AED≌△ACD,可得∠AED=∠C=2∠B,ED=CD,可证得△BDE为等腰三角形,所以有BE=DE=CD,可得结论.
解答 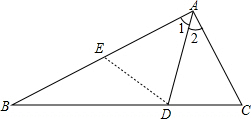 证明:在AB上取点E,使得AE=AC,
证明:在AB上取点E,使得AE=AC,
在△AED和△ACD中
$\left\{\begin{array}{l}{AE=AC}\\{∠1=∠2}\\{AD=AD}\end{array}\right.$,
∴△AED≌△ACD(SAS),
∴∠AED=∠C,AE=AC,ED=CD,
∵∠C=2∠B,且∠AED=∠B+∠BDE,
∴∠B=∠BDE,
∴BE=DE,
∴AB=AE+BD=AC+DE=AC+CD.
点评 本题主要考查三角形全等的判定和性质,解题的关键是构造全等三角形,在证明两条线段的和等于一条线段时,通常是截取线段,难度不大.


科目:初中数学 来源: 题型:解答题
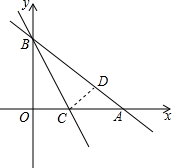 如图,一次函数的图象与x轴、y轴分别交于A、B两点,且A、B两点的坐标分别为(4,0),(0,3).
如图,一次函数的图象与x轴、y轴分别交于A、B两点,且A、B两点的坐标分别为(4,0),(0,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
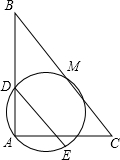 已知,如图所示,在△ABC中,∠BAC=90°,M是BC的中点,过点A、M的圆交AB于点D,过点D作DE∥BC交圆于点E,求证:DE=$\frac{1}{2}BC$.
已知,如图所示,在△ABC中,∠BAC=90°,M是BC的中点,过点A、M的圆交AB于点D,过点D作DE∥BC交圆于点E,求证:DE=$\frac{1}{2}BC$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
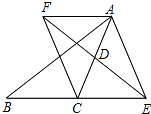 已知,如图,△ABC中,D是AC的中点,E是线段BC延长线上一点,过点A作BE的平行线与线段ED的延长线交于点F,连结AE、CF,求证:CF∥AE.
已知,如图,△ABC中,D是AC的中点,E是线段BC延长线上一点,过点A作BE的平行线与线段ED的延长线交于点F,连结AE、CF,求证:CF∥AE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
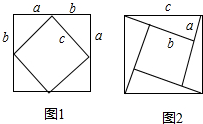 勾股定理被誉为千古第一定理长期以来人们对他进行了大量的研究找到了数百种不同的验证方法这些方法不但验证了勾股定理而且丰富了研究数学问题的方法和手段促进了数学的发展请同学们利用图一图二分别证明勾股定理.
勾股定理被誉为千古第一定理长期以来人们对他进行了大量的研究找到了数百种不同的验证方法这些方法不但验证了勾股定理而且丰富了研究数学问题的方法和手段促进了数学的发展请同学们利用图一图二分别证明勾股定理.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com