
 如图,AE=CF,∠AFD=∠CEB,添加下列一个条件后,不能判定△ADF≌△CBE的是( )
如图,AE=CF,∠AFD=∠CEB,添加下列一个条件后,不能判定△ADF≌△CBE的是( )| A. | ∠A=∠C | B. | BE=DF | C. | AD∥BC | D. | AD=CB |
科目:初中数学 来源: 题型:解答题
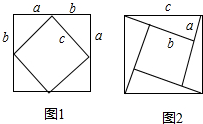 勾股定理被誉为千古第一定理长期以来人们对他进行了大量的研究找到了数百种不同的验证方法这些方法不但验证了勾股定理而且丰富了研究数学问题的方法和手段促进了数学的发展请同学们利用图一图二分别证明勾股定理.
勾股定理被誉为千古第一定理长期以来人们对他进行了大量的研究找到了数百种不同的验证方法这些方法不但验证了勾股定理而且丰富了研究数学问题的方法和手段促进了数学的发展请同学们利用图一图二分别证明勾股定理.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com