Question

13．如图1将矩形ABCD折叠，使得顶点B落在CD边上的P点处，已知折痕与边BC交于点O，连结AP、OP、OA．
（1）求证：△OCP∽△PDA；
（2）如图2，擦去折痕AO、线段OP，连结BP．动点M在线段AP上（点M与点P、A不重合），动点N在线段AB的延长线上，且BN=PM，连结MN交PB于点F，作ME⊥BP于点E．探究：当点M、N在移动过程中，线段EF与线段PB有何数量关系？并说明理由．

Answer 1

分析 （1）根据折叠的性质得到∠APO=∠B=90°，根据相似三角形的判定定理证明△OCP∽△PDA；
（2）作MQ∥AB交PB于Q，根据等腰三角形的性质和相似三角形的性质得到EF=$\frac{1}{2}$PB．

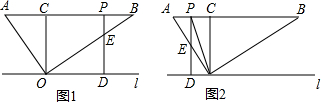
解答 解：（1）如图1，∵四边形ABCD是矩形，
∴AD=BC，DC=AB，∠DAB=∠B=∠C=∠D=90°．
由折叠可得：AP=AB，PO=BO，∠PAO=∠BAO，∠APO=∠B，
∴∠APO=90°．
∴∠APD=90°-∠CPO=∠POC，
∴△OCP∽△PDA；

（2）作MQ∥AN，交PB于点Q，如图2，
∵AP=AB，MQ∥AN，
∴∠APB=∠ABP，∠ABP=∠MQP，
∴∠APB=∠MQP，
∴MP=MQ，
∵MP=MQ，ME⊥PQ，
∴PE=EQ=$\frac{1}{2}$PQ，
∵BN=PM，MP=MQ，
∴BN=QM，
∵MQ∥AN，
∴∠QMF=∠BNF，
在△MFQ和△NFB中，$\left\{\begin{array}{l}{∠QMF=∠BNF}\\{∠QFM=∠BFN}\\{QM=BN}\end{array}\right.$，
∴△MFQ≌△NFB，
∴QF=BF，
∴QF=$\frac{1}{2}$QB，
∴EF=EQ+QF=$\frac{1}{2}$PQ+$\frac{1}{2}$QB=$\frac{1}{2}$PB．

点评 本题考查的是矩形的性质、折叠的性质、相似三角形的判定和性质、等腰三角形的性质以及勾股定理的应用，掌握折叠是一种轴对称，折叠前后的图形对应角相等、对应边相等，灵活运用相关的性质是解题的关键．