
 ��ͼ��������A���ʾ��a��B���ʾ��b��a��b����|a+2|+|b-4|=0��
��ͼ��������A���ʾ��a��B���ʾ��b��a��b����|a+2|+|b-4|=0������ ��1�����ݷǸ������������a=-2��b=4��
��2���ټ���ԭ��ľ���=�����˶���·��+OA�ij�������ԭ��ľ���������������������ӵ�B����ʼ�����˶���һֱ��ԭ��O����ʱOB�ij���-�����˶���·�̼�Ϊ����ԭ��ľ��룻���������ԭ��O����ʼ�����˶�����ʱ�����˶���·��-OB�ij��ȼ�Ϊ����ԭ��ľ��룻
�ڷ��������������0��t��2������t��2�����ݼס�����С��ԭ��ľ�������г�����t�ķ��̣��ⷽ�̼��ɣ�
��� �⣺��1����|a+2|+|b-4|=0��
��a+2=0��b-4=0��
��ã�a=-2��b=4��
���A��ʾ����Ϊ-2����B��ʾ����Ϊ4��
��2���ٵ�t=1ʱ����С��ԭ��ľ���Ϊ2+1=3����С��ԭ��ľ���Ϊ4-2=2����t=3ʱ����С��ԭ��ľ���Ϊ2+3=5����С��ԭ��ľ���Ϊ2��3-4=2��
�ڵ�0��t��2ʱ����t+2=4-2t��
���t=$\frac{2}{3}$��
��t��2ʱ����t+2=2t-4��
���t=6��
�ʵ�t=$\frac{2}{3}$���t=6��ʱ��������С��ԭ��ľ�����ȣ�
�ʴ�Ϊ����1��-2��4 ��2����3��2��5��2��
���� ���⿼���˷Ǹ��������ʣ�һԪһ�η��̵����ã��Լ����ᣬ�����ľ��룬����������˼�롢����˼�뼰���ν��˼���ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
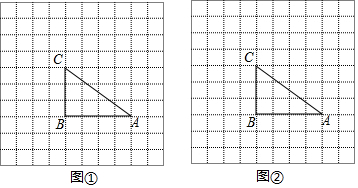
 ��ͼ����֪�����ϵ�A��ʾ����Ϊ-7����B��ʾ����Ϊ5����C����A����B�ľ�����ȣ�����P�ӵ�A��������ÿ��2����λ���ȵ��ٶ����������������˶������˶���ʱ��Ϊt��t��0���룮
��ͼ����֪�����ϵ�A��ʾ����Ϊ-7����B��ʾ����Ϊ5����C����A����B�ľ�����ȣ�����P�ӵ�A��������ÿ��2����λ���ȵ��ٶ����������������˶������˶���ʱ��Ϊt��t��0���룮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
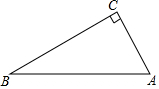 ��ͼ���ڡ�ABC�У���C=90�㣬��A����B��
��ͼ���ڡ�ABC�У���C=90�㣬��A����B���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com