Question

【题目】已知a，b，c为正数，满足如下两个条件：a+b+c=32 ①② 是否存在以 为三边长的三角形？如果存在，求出三角形的最大内角．

Answer 1

【答案】以 ,, 为三边长可构成一个直角三角形，它的最大内角为90°

【解析】试题分析：两个方程，有三个未知量，不能解出具体数值，但是能求出a,b,c关系，本题利用代入，因式分解，求出a,b,c关系.

试题解析：

解法1：将①②两式相乘，得.

即： =0,

即 =0,

=0,

即 ,

即 ,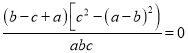

即 ,

所以b﹣c+a=0或c+a﹣b=0或c﹣a+b=0，

即b+a=c或c+a=b或c+b=a ．

因此，以， ， 为三边长可构成一个直角三角形，它的最大内角为90°．

解法2：结合①式，由②式可得得 1024-2(a2+b2+c2)= ,

又由①式得（a+b+c）2=1024，即a2+b2+c2=1024﹣2（ab+bc+ca），

代入③式，得 1024-2[1024-2(ab+bc+ca)]= ，

即abc=16（ab+bc+ca）﹣4096．

（a﹣16）（b﹣16）（c﹣16）=abc﹣16（ab+bc+ca）+256（a+b+c）﹣163=﹣4096+256×32﹣163=0，

所以a=16或b=16或c=16．

结合①式可得b+a=c或c+a=b或c+b=a ．

因此，以 ， ， 为三边长可构成一个直角三角形，它的最大内角为90°．