
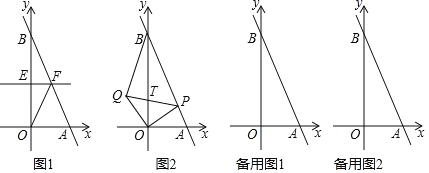
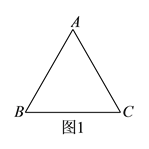
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨“—÷™B£®0£¨b£©£®b£ĺ0£© «y÷Š…Ō“Ľ∂ĮĶ„£¨÷ĪŌŖlĺ≠ĻżĶ„A£®1£¨0£©ľįĶ„B£¨ĹęRt°ųABO’ŘĶĢ£¨ ĻĶ√Ķ„B”ŽĶ„O÷ōļŌ£¨’ŘļŘ∑÷ĪūĹĽy÷Š°Ę÷ĪŌŖAB”ŕĶ„E°ĘF£¨Ń¨Ĺ”OF£ģ
£®1£©ĶĪb£Ĺ2 Ī£¨«ů÷ĪŌŖlĶńļĮ żĹ‚őŲ Ĺ£Ľ
£®2£©«Ž”√ļ¨”–◊÷ńłbĶńīķ ż ĹĪŪ ĺŌŖ∂őOFĶń≥§£¨≤ĘňĶ√ųŌŖ∂őOF”ŽŌŖ∂őABĶń żŃŅĻōŌĶ£Ľ
£®3£©»ÁÕľ£¨‘ŕ£®1£©ĶńŐűľĢŌ¬£¨…ŤĶ„P «ŌŖ∂őAB…Ō“Ľ∂ĮĶ„£®≤Ľ”ŽA°ĘB÷ōļŌ£©£¨ĹęŌŖ∂őOP»∆Ķ„Ońś Ī’Ž–ż◊™90°„÷ŃOQ£¨Ń¨ĹŠBQ°ĘPQ£¨PQĹĽy÷Š”ŕĶ„T£¨…ŤĶ„PĶńļŠ◊ÝĪÍő™t£ģ
ĘŔĶĪ°ųOPQĶń√śĽż◊Ó–° Ī£¨«ůTĶń◊ÝĪÍ£Ľ
Ęŕ»Ű°ųOPB «Ķ»—Ł»żĹ«–ő£¨«Ž÷ĪĹ”–ī≥Ų¬ķ◊„ŐűľĢĶńtĶń÷Ķ£Ľ
Ęػ۰ųOQB «÷ĪĹ«»żĹ«–ő£¨«Ž÷ĪĹ”–ī≥Ų¬ķ◊„ŐűľĢĶńtĶń÷Ķ£ģ
°ĺīūįł°Ņ£®1£©y£Ĺ©Ā2x+2£Ľ£®2£©OF£Ĺ![]() £¨OF£Ĺ
£¨OF£Ĺ![]() AB£¨ľŻĹ‚őŲ£Ľ£®3£©ĘŔT£®0£¨
AB£¨ľŻĹ‚őŲ£Ľ£®3£©ĘŔT£®0£¨![]() £©£¨ĘŕtĶń÷Ķő™
£©£¨ĘŕtĶń÷Ķő™![]() ĽÚ
ĽÚ![]() £¨ĘŘtĶń÷Ķő™1©Ā
£¨ĘŘtĶń÷Ķő™1©Ā![]() .
.
°ĺĹ‚őŲ°Ņ
£®1£©ņŻ”√īż∂®ŌĶ ż∑®ľīŅ…Ĺ‚ĺŲő Ő‚£Ľ
£®2£©ņŻ”√ĻīĻ…∂®ņŪ«ů≥ŲAB£¨ņŻ”√÷ĪĹ«»żĹ«–ő–ĪĪŖ÷–ŌŖĶń–‘÷ ľīŅ…Ĺ‚ĺŲő Ő‚£Ľ
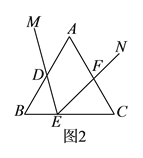
£®3£©ĘŔłýĺ›īĻŌŖ∂ő◊Ó∂ŐŅ…÷™£¨ĶĪOP°ÕAB Ī£¨°ųOPQĶń√śĽż◊Ó–°£¨«ů≥ŲP£¨QĶń◊ÝĪÍ£¨«ů≥Ų÷ĪŌŖPQĶńĹ‚őŲ ĹľīŅ…Ĺ‚ĺŲő Ő‚£ĽĘŕ∑÷ŃĹ÷÷«ť–ő∑÷Īū«ůĹ‚ľīŅ…Ĺ‚ĺŲő Ő‚£ĽĘŘ»ÁÕľ5÷–£¨»°OBĶń÷–Ķ„G£¨Ń¨Ĺ”BG£ģ…ŤP£®t£¨-2t+2£©£¨«ů≥ŲĶ„Q◊ÝĪÍ£¨łýĺ›QG=1ĻĻĹ®∑Ĺ≥ŐľīŅ…Ĺ‚ĺŲő Ő‚£ģ
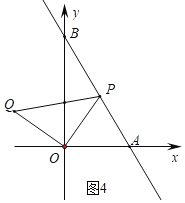
£®1£©»ÁÕľ1÷–£¨
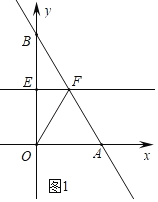
”…Ő‚“‚A£®1£¨0£©£¨B£®0£¨2£©£¨…Ť÷ĪŌŖABĶńĹ‚őŲ Ĺő™y£Ĺkx+b£¨‘Ú”–![]() £¨
£¨
Ĺ‚Ķ√![]() £¨
£¨
°ŗ÷ĪŌŖlĶńĹ‚őŲ Ĺő™y£Ĺ©Ā2x+2£Ľ
£®2£©»ÁÕľ1÷–£¨°ŖOB£Ĺb£¨OA£Ĺ1£¨
°ŗAB£Ĺ![]() £¨
£¨
°ŖEFīĻ÷Ī∆Ĺ∑÷ŌŖ∂őBO£¨
°ŗBF£ĹFO£¨
°ŖEF°őOA£¨
°ŗBF£ĹAF£¨
°ŗOF£Ĺ![]() AB£Ĺ
AB£Ĺ![]() £Ľ
£Ľ
£®3£©ĘŔ»ÁÕľ2÷–£¨◊ųPE°Õx÷Š”ŕE£¨QF°Õx÷Š”ŕF£ģ
°Ŗ°ųPOQ «Ķ»—Ł÷ĪĹ«»żĹ«–ő£¨
°ŗĶĪOPĶń÷Ķ◊Ó–° Ī£¨°ųPOQĶń√śĽż◊Ó–°£¨
łýĺ›īĻŌŖ∂ő◊Ó∂ŐŅ…÷™£¨ĶĪOP°ÕAB Ī£¨°ųOPQĶń√śĽż◊Ó–°£¨
°Ŗ÷ĪŌŖOPĶńĹ‚őŲ Ĺő™y£Ĺ![]() x£¨
x£¨
”… £¨
£¨
Ĺ‚Ķ√![]() £¨
£¨
°ŗP£®![]() £¨
£¨![]() £©£¨
£©£¨
°ŗOE£Ĺ![]() £¨PE£Ĺ
£¨PE£Ĺ![]() £¨
£¨
°Ŗ°ŌPEO£Ĺ°ŌQFO£Ĺ°ŌPOQ£Ĺ90°„£¨
°ŗ°ŌPOE+°ŌQOF£Ĺ90°„£¨°ŌPOE+°ŌOPE£Ĺ90°„£¨
°ŗ°ŌQOF£Ĺ°ŌOPE£¨
°ŖOP£ĹOQ£¨
°ŗ°ųOEP°’°ųQFO£®AAS£©£¨
°ŗQF£ĹOE£Ĺ![]() £¨OF£ĹPE£Ĺ
£¨OF£ĹPE£Ĺ![]() £¨
£¨
°ŗQ£®©Ā![]() £¨
£¨![]() £©£¨
£©£¨
°ŗ÷ĪŌŖPQĶńĹ‚őŲ Ĺő™y£Ĺ©Ā![]() x+
x+![]() £¨
£¨
°ŗT£®0£¨![]() £©£Ľ
£©£Ľ
Ęŕ»ÁÕľ3÷–£¨ĶĪBP£ĹOB£Ĺ2 Ī£¨◊ųPE°ÕOA”ŕE£ģ
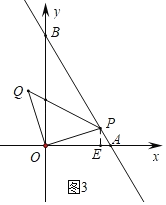
°ŖPE°őOB£¨
°ŗ![]() £Ĺ
£Ĺ![]() £Ĺ
£Ĺ![]() £¨
£¨
°ŗ![]() £Ĺ
£Ĺ![]() £Ĺ
£Ĺ![]() £¨
£¨
°ŗPE£Ĺ![]() £¨AE£Ĺ
£¨AE£Ĺ![]() £¨
£¨
°ŗOE£Ĺ1©Ā![]() £Ĺ
£Ĺ![]() £ģ
£ģ
°ŗt£Ĺ![]() £ģ
£ģ
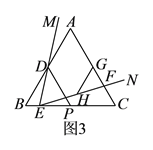
»ÁÕľ4÷–£¨ĶĪPB£ĹPA Ī£¨OP£ĹPB¬ķ◊„ŐűľĢ£¨īň Īt£Ĺ![]() £ģ
£ģ
◊Ř…Ōňý Ų£¨¬ķ◊„ŐűľĢĶńtĶń÷Ķő™![]() ĽÚ
ĽÚ![]() £Ľ
£Ľ
ĘŘ»ÁÕľ5÷–£¨»°OBĶń÷–Ķ„G£¨Ń¨Ĺ”BG£ģ…ŤP£®t£¨©Ā2t+2£©£¨
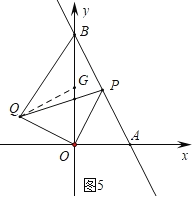
“◊÷™Q£®2t©Ā2£¨t£©£¨G£®0£¨1£©ĶĪ°ŌOQB£Ĺ90°„ Ī£¨
°ŖGB£ĹOG£¨
°ŗQG£Ĺ![]() OB£Ĺ1£¨
OB£Ĺ1£¨
°ŗ£®2t©Ā2£©2+£®t©Ā1£©2£Ĺ1£¨
Ĺ‚Ķ√t£Ĺ1©Ā![]() ĽÚ1+
ĽÚ1+![]() £®…Š∆ķ£©£¨
£®…Š∆ķ£©£¨
°ŗ¬ķ◊„ŐűľĢĶńtĶń÷Ķő™1©Ā![]() £ģ
£ģ


 ŐžŐžŌÚ…Ō“ĽĪĺļ√ĺŪŌĶŃ–īūįł
ŐžŐžŌÚ…Ō“ĽĪĺļ√ĺŪŌĶŃ–īūįł –°—ß…ķ10∑÷÷””¶”√Ő‚ŌĶŃ–īūįł
–°—ß…ķ10∑÷÷””¶”√Ő‚ŌĶŃ–īūįł
| ńÍľ∂ | łŖ÷–Ņő≥Ő | ńÍľ∂ | ≥ű÷–Ņő≥Ő |
| łŖ“Ľ | łŖ“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű“Ľ | ≥ű“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ∂Ģ | łŖ∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű∂Ģ | ≥ű∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ»ż | łŖ»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű»ż | ≥ű»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° |
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņń≥—ß–£ő™Ńň«ž◊£–£‘į“’ űĹŕ,◊ľĪłĻļ¬Ú“ĽŇķŇŤĽ®≤ľ÷√–£‘į.“—÷™1ŇŤA÷÷Ľ®ļÕ2ŇŤB÷÷Ľ®“ĽĻ≤–Ť13‘™,2ŇŤA÷÷Ľ®ļÕ1ŇŤB÷÷Ľ®“ĽĻ≤–Ť11‘™.
(1)«ů1ŇŤA÷÷Ľ®ļÕ1ļ–B÷÷Ľ®Ķń ؾسų «∂ŗ…Ŕ‘™?
(2)—ß–£◊ľĪłĻļĹÝ’‚ŃĹ÷÷ŇŤĽ®Ļ≤100ŇŤ,≤Ę«“A÷÷ŇŤĽ®Ķń żŃŅ≤Ľ≥¨ĻżB÷÷ŇŤĽ® żŃŅĶń2Ī∂,«Ž«ů≥ŲA÷÷ŇŤĽ®Ķń żŃŅ◊Ó∂ŗ «∂ŗ…Ŕ?
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ”–ňńłŲ»żĹ«–ő£¨∑÷Īū¬ķ◊„Ō¬Ń–ŐűľĢ£ļ£®1£©“ĽłŲĹ«Ķ»”ŕŃŪÕ‚ŃĹłŲńŕĹ«÷ģļÕ£Ľ£®2£©»żłŲńŕĹ«÷ģĪ»ő™3£ļ4£ļ5£Ľ£®3£©»żĪŖ÷ģĪ»ő™5£ļ12£ļ13£Ľ£®4£©»żĪŖ≥§∑÷Īūő™5£¨24£¨25£ģ∆š÷–÷ĪĹ«»żĹ«–ő”–£®°°°°£©
A. 1łŲB. 2łŲC. 3łŲD. 4łŲ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
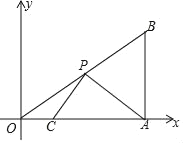
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨‘ŕ°ųABC÷–£¨°ŌA£Ĺ90°„£¨P «BC…Ō“ĽĶ„£¨«“DB£ĹDC£¨ĻżBC…Ō“ĽĶ„P£¨◊ųPE°ÕAB”ŕE£¨PF°ÕDC”ŕF£¨“—÷™£ļAD£ļDB£Ĺ1£ļ3£¨BC£Ĺ![]() £¨‘ÚPE+PFĶń≥§ «£® £©
£¨‘ÚPE+PFĶń≥§ «£® £©

A. ![]() B. 6C.
B. 6C. ![]() D.
D. ![]()
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ—ß–£ ≥Ő√≥Ý∑ŅĶń◊ņ◊”…Ō’Ż∆ŽĶōįŕ∑Ň◊һ۳…ŌŗÕ¨ĻśłŮĶńĶķ◊”£¨Ķķ◊”ĶńłŲ ż”ŽĶķ◊”ĶńłŖ∂»ĶńĻōŌĶ»ÁŌ¬ĪŪ£ļ


£®1£©ĶĪ◊ņ◊”…Ō∑Ň”–x£®łŲ£©Ķķ◊” Ī£¨«Ž–ī≥Ųīň ĪĶķ◊”ĶńłŖ∂»£®”√ļ¨xĶń Ĺ◊”ĪŪ ĺ£©£Ľ
£®2£©∑÷Īūī”»żłŲ∑ĹŌÚ…ŌŅī£¨∆š»ż ”Õľ»Á…ŌÕľňý ĺ£¨≥Ý∑Ņ ¶łĶŌŽį—ňŁ√«’Ż∆ŽĶĢ≥…“ĽřŻ£¨«ůĶĢ≥…“ĽřŻļůĶńłŖ∂»£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™’ż∑ĹŐŚĶńĪŖ≥§ő™a£ģ
£®1£©“ĽłŲ’ż∑ĹŐŚĶńĪŪ√śĽż «∂ŗ…Ŕ£ŅŐŚĽż «∂ŗ…Ŕ£Ņ
£®2£©2łŲ’ż∑ĹŐŚ£®»ÁÕľĘŕ£©ĶĢ∑Ň‘ŕ“Ľ∆ū£¨ňŁĶńĪŪ√śĽż «∂ŗ…Ŕ£ŅŐŚĽż «∂ŗ…Ŕ£Ņ
£®3£©nłŲ’ż∑ĹŐŚįī’’ÕľĘŕĶń∑Ĺ ĹĶĢ∑Ň‘ŕ“Ľ∆ū£¨ňŁĶńĪŪ√śĽż «∂ŗ…Ŕ£ŅŐŚĽż «∂ŗ…Ŕ£Ņ

≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ‘ŕ∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶ÷–£¨Rt°ųOABĶń∂•Ķ„A‘ŕx÷ŠĶń’żįŽ÷Š…Ō£¨∂•Ķ„BĶń◊ÝĪÍő™(3£¨![]() )£¨Ķ„CĶń◊ÝĪÍő™(1£¨0)£¨Ķ„Pő™–ĪĪŖOB…ŌĶń“Ľ∂ĮĶ„£¨‘ÚPA+PCĶń◊Ó–°÷Ķ_____£ģ
)£¨Ķ„CĶń◊ÝĪÍő™(1£¨0)£¨Ķ„Pő™–ĪĪŖOB…ŌĶń“Ľ∂ĮĶ„£¨‘ÚPA+PCĶń◊Ó–°÷Ķ_____£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ‘ŕĶ»ĪŖ![]() ÷–£¨
÷–£¨![]() £¨Ķ„
£¨Ķ„![]() ő™
ő™![]() Ķń÷–Ķ„£¨Ķ„
Ķń÷–Ķ„£¨Ķ„![]() «
«![]() ĪŖ…Ō“Ľ∂ĮĶ„£¨
ĪŖ…Ō“Ľ∂ĮĶ„£¨![]() £¨«“
£¨«“![]() ĶńŃĹĪŖ∑÷Īū”Ž
ĶńŃĹĪŖ∑÷Īū”Ž![]() ĶńĪŖ
ĶńĪŖ![]() £¨
£¨![]() ĹĽ”ŕĶ„
ĹĽ”ŕĶ„![]() £¨
£¨![]() £®Ķ„
£®Ķ„![]() ≤Ľ”ŽĶ„
≤Ľ”ŽĶ„![]() £¨
£¨![]() ÷ōļŌ£©£ģ
÷ōļŌ£©£ģ
£®![]() £©ĶĪ
£©ĶĪ![]() Ī£¨«Ž‘ŕÕľ
Ī£¨«Ž‘ŕÕľ![]() ÷–≤Ļ»ęÕľ–ő£ģ
÷–≤Ļ»ęÕľ–ő£ģ
£®![]() £©‘ŕÕľ
£©‘ŕÕľ![]() ÷–£¨…Ť
÷–£¨…Ť![]() Ķń≥§ő™
Ķń≥§ő™![]() £¨
£¨![]() Ķń≥§ő™
Ķń≥§ő™![]() £¨«ů
£¨«ů![]() ”Ž
”Ž![]() ĶńļĮ żĻōŌĶ Ĺ£¨≤Ę–ī≥Ų◊‘ĪšŃŅ
ĶńļĮ żĻōŌĶ Ĺ£¨≤Ę–ī≥Ų◊‘ĪšŃŅ![]() Ķń»°÷Ķ∑∂őߣģ
Ķń»°÷Ķ∑∂őߣģ
£®![]() £©»ÁÕľ
£©»ÁÕľ![]() £¨Ķ„
£¨Ķ„![]() £¨
£¨![]() ∑÷Īūő™
∑÷Īūő™![]() £¨
£¨![]() Ķń÷–Ķ„£¨‘ŕ
Ķń÷–Ķ„£¨‘ŕ![]() …ŌĹō»°
…ŌĹō»°![]() £¨Ń¨Ĺ”
£¨Ń¨Ĺ”![]() £¨
£¨![]() £ģ«Ž÷§√ų
£ģ«Ž÷§√ų![]() £ģ
£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨Rt°ųABOĶń∂•Ķ„A£®a°Ęb£© «“ĽīőļĮ ży=x+mĶńÕľŌŮ”Ž∑īĪ»ņżļĮ ż![]() ĶńÕľŌŮ‘ŕĶŕ“ĽŌůŌřĶńĹĽĶ„£¨«“S°ųABO£Ĺ3°£
ĶńÕľŌŮ‘ŕĶŕ“ĽŌůŌřĶńĹĽĶ„£¨«“S°ųABO£Ĺ3°£

ĘŔłýĺ›’‚–©ŐűľĢń„ń‹ĻĽ«ů≥Ų∑īĪ»ņżļĮ żĶńĹ‚őŲ Ŭū£Ņ»ÁĻŻń‹ĻĽ£¨«Žń„«ů≥Ųņī£¨»ÁĻŻ≤Ľń‹£¨«ŽňĶ√ųņŪ”…°£
Ęŕń„ń‹ĻĽ«ů≥Ų“ĽīőļĮ żĶńļĮ żĻōŌĶ Ŭū£Ņ»ÁĻŻń‹£¨«Žń„«ů≥Ųņī£¨»ÁĻŻ≤Ľń‹£¨«Žń„ňĶ√ųņŪ”…°£
≤ťŅīīūįłļÕĹ‚őŲ>>
Ļķľ —ß–£”Ň—° - Ń∑Ōį≤ŠŃ–ĪŪ - ‘Ő‚Ń–ĪŪ
ļĢĪĪ °Ľ•Ń™ÕÝő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®∆ĹŐ® | ÕÝ…Ō”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | ĶÁ–Ň’©∆≠ĺŔĪ®◊®«Ý | …śņķ ∑–ťőř÷ų“Ś”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | …ś∆ů«÷»®ĺŔĪ®◊®«Ý
ő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®ĶÁĽį£ļ027-86699610 ĺŔĪ®” Ōš£ļ58377363@163.com