练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在△ABC中，∠A＝90°，P是BC上一点，且DB＝DC，过BC上一点P，作PE⊥AB于E，PF⊥DC于F，已知：AD：DB＝1：3，BC＝，则PE+PF的长是（ ）

    A. B. 6C. D.

    【答案】C

    【解析】

    根据三角形的面积判断出PE+PF的长等于AC的长，这样就变成了求AC的长；在Rt△ACD和Rt△ABC中，利用勾股定理表示出AC，解方程就可以得到AD的长，再利用勾股定理就可以求出AC的长，也就是PE+PF的长．

    ∵△DCB为等腰三角形，PE⊥AB，PF⊥CD，AC⊥BD，

    ∴S△BCD=BDPE+CDPF=BDAC，

    ∴PE+PF=AC，

    设AD=x，BD=CD=3x，AB=4x，

    ∵AC2=CD2-AD2=（3x）2-x2=8x2，

    ∵AC2=BC2-AB2=（）2-（4x）2，

    ∴x=2，

    ∴AC=4，

    ∴PE+PF=4．

    故选：C

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在平行四边形ABCD中，∠B=∠AFE，EA是∠BEF的平分线，求证：

    (1)△ABE≌△AFE；

    (2)∠FAD=∠CDE.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

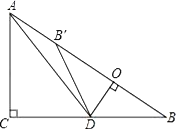
    【题目】如图，在Rt△ABC中，∠ACB=90°，AC=6，BC=8，点D为边CB上的一个动点（点D不与点B重合），过D作DO⊥AB，垂足为O，点B′在边AB上，且与点B关于直线DO对称，连接DB′，AD．

    （1）求证：△DOB∽△ACB；

    （2）若AD平分∠CAB，求线段BD的长；

    （3）当△AB′D为等腰三角形时，求线段BD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】据调查，初中学生课桌椅不合格率达76.7%（不合格是指不能按照学生不同的身高来调节课桌椅的高度），为了解初中生的身高情况，随机抽取了某校初中部分男生、女生进行调查收集数据如下：

    男生身高（单位：cm）：163 161 160 163 161 162 163 164 163 163

    女生身高（单位：cm）：164 161 160 161 161 162 160 162 163 162

    整理数据：

    160

    161

    162

    163

    164

    男生（人）

    1

    2

    1

    a

    1

    女生（人）

    2

    b

    3

    1

    1

    根据以上信息，解答下列问题：

    （1）填空：a＝　 ，b＝　 ，并补全条形统计图；

    （2）现有两名身高都为163cm的男生和女生，比较这两名同学分别在男生、女生中的身高情况，并简述理由；

    （3）根据相关研究发现，只有身高为161cm的初中生课桌椅是合格的，试估计全校1000名学生中，有多少名学生的课桌椅是合格的？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】直线AB∥CD，直线EF分别交AB、CD于点A、C，CM是∠ACD的平分线，CM交AB于点N．

    （1）如图①，过点A作AC的垂线交CM于点M，若∠MCD＝55°，求∠MAN的度数；

    （2）如图②，点G是CD上的一点，连接MA、MG，若MC平分∠AMG且∠AMG＝36°，∠MGD+∠EAB＝180°，求∠ACD的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在等腰三角形ABC中，AB=AC，以底边BC的垂直平分线和BC所在的直线建立平面直角坐标系，抛物线y=﹣x2+x+4经过A、B两点．

    （1）写出点A、点B的坐标；

    （2）若一条与y轴重合的直线l以每秒2个单位长度的速度向右平移，分别交线段OA、CA和抛物线于点E、M和点P，连接PA、PB．设直线l移动的时间为t（0＜t＜4）秒，求四边形PBCA的面积S（面积单位）与t（秒）的函数关系式，并求出四边形PBCA的最大面积；

    （3）在（2）的条件下，是否存在t，使得△PAM是直角三角形？若存在，请求出点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

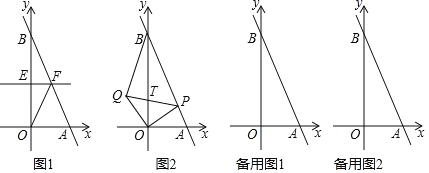
    【题目】如图，已知B（0，b）（b＞0）是y轴上一动点，直线l经过点A（1，0）及点B，将Rt△ABO折叠，使得点B与点O重合，折痕分别交y轴、直线AB于点E、F，连接OF．

    （1）当b＝2时，求直线l的函数解析式；

    （2）请用含有字母b的代数式表示线段OF的长，并说明线段OF与线段AB的数量关系；

    （3）如图，在（1）的条件下，设点P是线段AB上一动点（不与A、B重合），将线段OP绕点O逆时针旋转90°至OQ，连结BQ、PQ，PQ交y轴于点T，设点P的横坐标为t．

    ①当△OPQ的面积最小时，求T的坐标；

    ②若△OPB是等腰三角形，请直接写出满足条件的t的值；

    ③若△OQB是直角三角形，请直接写出满足条件的t的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

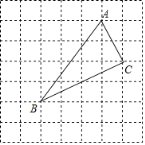
    【题目】如图，在7×7网格中，每个小正方形的边长都为1．

    (1)建立适当的平面直角坐标系后，若点A(1，3)、C(2，1)，则点B的坐标为______；

    (2)△ABC的面积为______；

    (3)判断△ABC的形状，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知一次函数y=kx+b 的图象与反比例函数y=的图交象于A、B两点，且点A的横坐标和点B的纵坐标都是－2 ， 求：

    （1）一次函数的解析式；

    （2）△AOB的面积

    查看答案和解析>>

    同步练习册答案