
【题目】如图,在平行四边形ABCD中,∠B=∠AFE,EA是∠BEF的平分线,求证:
(1)△ABE≌△AFE;
(2)∠FAD=∠CDE.

【答案】(1) 见解析 (2) 见解析
【解析】【试题分析】(1)利用AAS判定证明即可;(2)在平行四边形ABCD中,根据平行四边形的性质得:AD∥BC,根据两直线平行,内错角相等得:∠ADF=∠DEC.
得:∠AFD=∠C.
在△ADF与△DEC中,由三角形内角和定理,∠FAD=∠CDE.得证.
【试题解析】
(1)在△ABE与△AFE中,∠B=∠AFE,∠AEB=∠AEF,AE=AE,∴△ABE≌△AFE(AAS);
(2)平行四边形ABCD中,∵AD∥BC,∴∠ADF=∠DEC.
∵AB∥CD,∴∠C=180°-∠B.
又∠AFD=180°-∠AFE,∠B=∠AFE,
∴∠AFD=∠C.
在△ADF与△DEC中,由三角形内角和定理,得∠FAD=180°-∠ADF-∠AFD,∠CDE=180°-∠DEC-∠C,
∴∠FAD=∠CDE.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A的坐标为(m,m),点B的坐标为(n,﹣n),抛物线经过A、O、B三点,连接OA、OB、AB,线段AB交y轴于点C.已知实数m、n(m<n)分别是方程x2﹣2x﹣3=0的两根.
(1)求抛物线的解析式;
(2)若点P为线段OB上的一个动点(不与点O、B重合),直线PC与抛物线交于D、E两点(点D在y轴右侧),连接OD、BD.
①当△OPC为等腰三角形时,求点P的坐标;
②求△BOD 面积的最大值,并写出此时点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
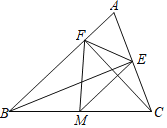
【题目】如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点,BC=10.
(1)若∠ABC=50°,∠ACB=60°,求∠EMF的度数;
(2)若EF=4,求△MEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】顺次连接四边形ABCD四边中点得到新的四边形为菱形,那么原四边形ABCD为( )
A. 矩形
B. 菱形
C. 对角线相等的四边形
D. 对角线垂直的四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个口袋中放有290个涂有红、黑、白三种色的质地相同的小球,若红球个数是黑球个数的2倍多3个,从袋中任取一个球是白球的概率是![]() .
.
(1)求袋中红球的个数.
(2)求从袋中任取一个球是黑球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】京沪高速公路全长1262千米,汽车沿京沪高速公路从上海驶往北京.
(1)那么汽车行驶全程所需时间t(小时)与行驶的平均速度v(千米/小时)之间有怎样的关系?t是v的什么函数?
(2)若平均速度为100千米/小时,大约需几个小时跑完全程?
(3)若跑完全程控制在10小时之内,那么车速应控制在什么范围内?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了庆祝校园艺术节,准备购买一批盆花布置校园.已知1盆A种花和2盆B种花一共需13元,2盆A种花和1盆B种花一共需11元.
(1)求1盆A种花和1盒B种花的售价各是多少元?
(2)学校准备购进这两种盆花共100盆,并且A种盆花的数量不超过B种盆花数量的2倍,请求出A种盆花的数量最多是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,AC=CB=2,以BC为边向外作正方形BCDE,动点M从A点出发,以每秒1个单位的速度沿着A→C→D的路线向D点匀速运动(M不与A、D重合);过点M作直线l⊥AD,l与路线A→B→D相交于N,设运动时间为t秒:
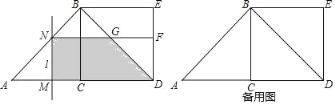
(1)填空:当点M在AC上时,BN= (用含t的代数式表示);
(2)当点M在CD上时(含点C),是否存在点M,使△DEN为等腰三角形?若存在,直接写出t的值;若不存在,请说明理由;
(3)过点N作NF⊥ED,垂足为F,矩形MDFN与△ABD重叠部分的面积为S,求S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=90°,P是BC上一点,且DB=DC,过BC上一点P,作PE⊥AB于E,PF⊥DC于F,已知:AD:DB=1:3,BC=![]() ,则PE+PF的长是( )
,则PE+PF的长是( )

A. ![]() B. 6C.
B. 6C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com