
【题目】京沪高速公路全长1262千米,汽车沿京沪高速公路从上海驶往北京.
(1)那么汽车行驶全程所需时间t(小时)与行驶的平均速度v(千米/小时)之间有怎样的关系?t是v的什么函数?
(2)若平均速度为100千米/小时,大约需几个小时跑完全程?
(3)若跑完全程控制在10小时之内,那么车速应控制在什么范围内?
科目:初中数学 来源: 题型:
【题目】某校七年级社会实践小组去某商场调查商品的销售情况,了解到该商场以每件80元的价格购进了某品牌衬衫500件,并以每件120元的价格销售了400件,商场准备采取促销措施,将剩下的衬衫降价销售.
(1)每件衬衫降价多少元时,销售完这批衬衫正好达到盈利45%的预期目标?
(2)在(1)的条件下,某公司给员工发福利,在该商场促销钱购买了20件该品牌的衬衫发给员工,后因为有新员工加入,又要购买5件该衬衫,购买这5件衬衫时恰好赶上该商场进行促销活动,求该公司购买这25件衬衫的平均价格.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,给出下列的条件,能判断它是平行四边形的是( )
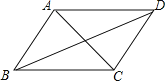
A. AB//CD, AD=BCB. ∠B=∠C,∠A=∠D
C. AB=AD, BC=CDD. AB=CD, AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算:(﹣2010)0+![]() ﹣2sin60°﹣3tan30°+
﹣2sin60°﹣3tan30°+![]() ;
;
(2)解方程:x2﹣6x+2=0;
(3)已知关于x的一元二次方程x2﹣mx﹣2=0.
①若﹣1是方程的一个根,求m的值和方程的另一根;
②证明:对于任意实数m,函数y=x2﹣mx﹣2的图象与x轴总有两个交点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l为正比例函数y=x的图象,点A1的坐标为(1,0),过点A1作x轴的垂线交直线l于点D1,以A1D1为边作正方形A1B1C1D1;过点C1作直线l的垂线,垂足为A2,交x轴于点B2,以A2B2为边作正方形A2B2C2D2;过点C2作x轴的垂线,垂足为A3,交直线l于点D3,以A3D3为边作正方形A3B3C3D3,…,按此规律操作下所得到的正方形AnBnCnDn的面积是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数y=3x+2的图象与y轴交于点A,与反比例函数y=![]() (k≠0)在第一象限内的图象交于点B,且点B的横坐标为1.过点A作AC⊥y轴交反比例函数y=
(k≠0)在第一象限内的图象交于点B,且点B的横坐标为1.过点A作AC⊥y轴交反比例函数y=![]() (k≠0)的图象于点C,连接BC.
(k≠0)的图象于点C,连接BC.
(1)求反比例函数的表达式.
(2)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在矩形ABCD中,对角线AC与BD相交于点O,过点O作直线EF⊥BD,且交AD于点E,交BC于点F,连接BE,DF,且BE平分∠ABD.
①求证:四边形BFDE是菱形;
②直接写出∠EBF的度数.
(2)把(1)中菱形BFDE进行分离研究,如图2,G,I分别在BF,BE边上,且BG=BI,连接GD,H为GD的中点,连接FH,并延长FH交ED于点J,连接IJ,IH,IF,IG.试探究线段IH与FH之间满足的关系,并说明理由;
(3)把(1)中矩形ABCD进行特殊化探究,如图3,矩形ABCD满足AB=AD时,点E是对角线AC上一点,连接DE,作EF⊥DE,垂足为点E,交AB于点F,连接DF,交AC于点G.请直接写出线段AG,GE,EC三者之间满足的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰三角形ABC中,AB=AC,以底边BC的垂直平分线和BC所在的直线建立平面直角坐标系,抛物线y=﹣![]() x2+
x2+![]() x+4经过A、B两点.
x+4经过A、B两点.

(1)写出点A、点B的坐标;
(2)若一条与y轴重合的直线l以每秒2个单位长度的速度向右平移,分别交线段OA、CA和抛物线于点E、M和点P,连接PA、PB.设直线l移动的时间为t(0<t<4)秒,求四边形PBCA的面积S(面积单位)与t(秒)的函数关系式,并求出四边形PBCA的最大面积;
(3)在(2)的条件下,是否存在t,使得△PAM是直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com