
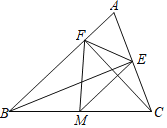
【题目】如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点,BC=10.
(1)若∠ABC=50°,∠ACB=60°,求∠EMF的度数;
(2)若EF=4,求△MEF的面积.
【答案】(1)∠EMF=40°;(2)2![]() .
.
【解析】
(1)根据直角三角形的性质得到BM=FM,根据等腰三角形的性质、三角形内角和定理计算;
(2)作MN⊥EF于N,根据直角三角形的性质得到FM=![]() BC=5,根据等腰三角形的性质、三角形面积公式计算.
BC=5,根据等腰三角形的性质、三角形面积公式计算.
解:(1)∵CF⊥AB,M为BC的中点,
∴BM=FM,
∵∠ABC=50°,
∴∠MFB=∠MBF=50°,
∴∠BMF=180°-2×50°=80°,
同理,∠CME═180°-2×60°=60°,
∴∠EMF=180°-∠BMF-∠CME=40°;
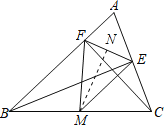
(2)作MN⊥EF于N,
∵CF⊥AB,M为BC的中点,
∴MF是Rt△BFC斜边上的中线,
∴FM=![]() BC=5,
BC=5,
同理可得,ME=5,
∴△EFM是等腰三角形,
∵EF=4,
∴FN=2,
∴MN=![]() =
=![]() ,
,
∴△EFM的面积=![]() EFMN=
EFMN=![]() ×4×
×4×![]() =2
=2![]() .
.


科目:初中数学 来源: 题型:
【题目】嘉淇乘坐一艘游船出海游玩,游船上的雷达扫描探测得到的结果如图所示,每相邻两个圆之间距离是1km (最小圆的半径是1km ),下列关于小艇 A , B 的位置描述,正确的是( )

A.小艇 A 在游船的北偏东60°方向上,且与游船的距离是3km
B.游船在小艇 A 的南偏西60°方向上,且与小艇 A 的距离是3km
C.小艇 B 在游船的北偏西30°方向上,且与游船的距离是 2km
D.游船在小艇 B 的南偏东60°方向上,且与小艇 B 的距离是 2km
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,点
,点![]() 分别在射线
分别在射线![]() 上运动(不与点
上运动(不与点![]() 重合)
重合)
观察:
(1)如图1,若![]() 和
和![]() 的平分线交于点
的平分线交于点![]() ,
,![]() _____°
_____°

猜想:
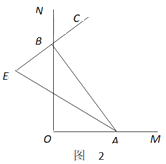
(2)如图2,随着点![]() 分别在射线
分别在射线![]() 上运动(不与点
上运动(不与点![]() 重合). 若
重合). 若![]() 是
是![]() 的平分线,
的平分线,![]() 的反向延长线与
的反向延长线与![]() 的平分线交于点
的平分线交于点![]() ,
, ![]() 的大小会变吗?如果不会,求
的大小会变吗?如果不会,求![]() 的度数;如果会改变,说明理由.
的度数;如果会改变,说明理由.
拓展:
(3)如图3,在(2)基础上,小明将![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在四边形
落在四边形![]() 内点
内点![]() ′的位置,求
′的位置,求![]() 的度数.
的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人相约元旦登山,甲、乙两人距地面的高度y(m)与登山时间x(min)之间的函数图像如图所示,根据图像所提供的信息解答下列问题:
(1)t= min.
(2)若乙提速后,乙登山的上升速度是甲登山的上升速度3倍,
①则甲登山的的上升速度是 m/min;
②请求出甲登山过程中,距地面的高度y(m)与登山时间x(min)之间的函数关系式.
③当甲、乙两人距地面高度差为70m时,求x的值(直接写出满足条件的x值).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某乒乓球的质量检验结果如下:
抽取的乒乓球数n | 50 | 100 | 200 | 500 | 1000 | 1500 | 2000 |
优等品的频数m | 48 | 95 | 188 | x | 948 | 1426 | 1898 |
优等品的频率 | 0.960 | y | 0.940 | 0.944 | z | 0.951 | 0.949 |
(1)根据表中信息可得:x=______,y=______,z=______;
(2)从这批乒乓球中,任意抽取一只乒乓球是优等品的概率的估计值是多少?(精确到0.01).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,给出下列的条件,能判断它是平行四边形的是( )
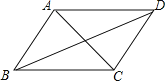
A. AB//CD, AD=BCB. ∠B=∠C,∠A=∠D
C. AB=AD, BC=CDD. AB=CD, AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
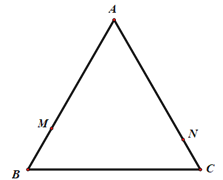
【题目】如图,等边△ABC的边长为8,动点M从点B出发,沿B→A→C→B的方向以每秒3个单位长度的速度运动,动点N从点C出发,沿C→A→B-C的方向以每秒2个单位长度的速度运动.
(1)若动点M、N同时出发,经过几秒第一次相遇?
(2)若动点M、N同时出发,且其中一点到达终点时,另一点即停止运动.在△ABC的边上是否存在一点D,使得以点A、M、N、D为顶点的四边形为平行四边形?若存在,求此时运动的时间![]() 及点D的具体位置;若不存在,请说明理由.
及点D的具体位置;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
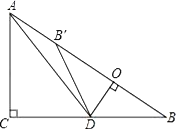
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D为边CB上的一个动点(点D不与点B重合),过D作DO⊥AB,垂足为O,点B′在边AB上,且与点B关于直线DO对称,连接DB′,AD.
(1)求证:△DOB∽△ACB;
(2)若AD平分∠CAB,求线段BD的长;
(3)当△AB′D为等腰三角形时,求线段BD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com