
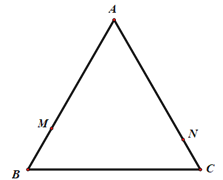
【题目】如图,等边△ABC的边长为8,动点M从点B出发,沿B→A→C→B的方向以每秒3个单位长度的速度运动,动点N从点C出发,沿C→A→B-C的方向以每秒2个单位长度的速度运动.
(1)若动点M、N同时出发,经过几秒第一次相遇?
(2)若动点M、N同时出发,且其中一点到达终点时,另一点即停止运动.在△ABC的边上是否存在一点D,使得以点A、M、N、D为顶点的四边形为平行四边形?若存在,求此时运动的时间![]() 及点D的具体位置;若不存在,请说明理由.
及点D的具体位置;若不存在,请说明理由.
【答案】(1)经过t=![]() s第一次相遇. (2)运动了
s第一次相遇. (2)运动了![]() 或
或![]() s时,A、M、N、D四点能够成平行四边形,此时点D在BC上,且BD=
s时,A、M、N、D四点能够成平行四边形,此时点D在BC上,且BD=![]() 或
或![]() .
.
【解析】
(1)设经过t秒钟两点第一次相遇,然后根据点M运动的路程+点N运动的路程=AB+CA列方程求解即可;
(2)首先根据题意画出图形:如图②,当0≤t≤![]() 时,AN+CN=MB+CN=8;当
时,AN+CN=MB+CN=8;当![]() <t≤4时,此时A、M、N三点在同一直线上,不能构成平行四边形;当4<t≤
<t≤4时,此时A、M、N三点在同一直线上,不能构成平行四边形;当4<t≤![]() 时,AN+NB=AN+AM=8;当
时,AN+NB=AN+AM=8;当![]() <t≤8时,△BNM为等边三角形,由BN=BM可求得t的值,可得此时M、N重合,不能构成平行四边形..
<t≤8时,△BNM为等边三角形,由BN=BM可求得t的值,可得此时M、N重合,不能构成平行四边形..
(1)由题意得:3t+2t=16,解得:t=![]() ;
;
答:若动点M、N同时出发,经过t=![]() s第一次相遇.
s第一次相遇.
(2)①当0≤t≤![]() 时,点M、N、D的位置如图2所示:
时,点M、N、D的位置如图2所示: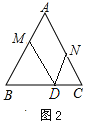
∵四边形ANDM为平行四边形,
∴DM=AN,DM∥AN.
∴∠MDB=∠C=60°
∵△ABC为等边三角形,
∴∠B=∠C=60°.
∴∠MDB =∠B.
∴MB=MD= AN
∴AN+CN=MB+CN=8,即:3t+2t=8,t=![]() ,
,
此时点D在BC上,且BD=![]() (或CD=
(或CD=![]() ),
),
②当![]() <t≤4时,此时A、M、N三点在同一直线上,不能构成平行四边形;
<t≤4时,此时A、M、N三点在同一直线上,不能构成平行四边形;
③4<t≤![]() 时,点M、N、D的位置如图所1示:
时,点M、N、D的位置如图所1示:
∵四边形ANDM为平行四边形,
∴DN=AM,AM∥DN.
∴∠NDB=∠C=60°
∵△ABC为等边三角形,
∴∠B=∠C =60°.
∴∠NDB=∠B.
∴BN=ND= AM.
∴AN+NB=AN+AM=8,2t-8+3t-8=8,解得:t=![]() ,
,
此时点D在BC上,且BD=![]() (或CD=
(或CD=![]() ),
),
④当![]() <t≤8时,点M、N、D的位置如图所3示:
<t≤8时,点M、N、D的位置如图所3示: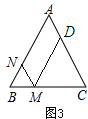
则BN=16-2t,BM=24-3t,
∵△ABC为等边三角形,
∴∠A=∠C=60°.
若MN∥AC,则∠BNM=∠A=60°, ∠BMN=∠C=60°
∴△BNM为等边三角形,
∴BN=BM,即:16-2t =24-3t,解得t=8,此时M、N重合,不能构成平行四边形.
答:运动了![]() 或
或![]() s时,A、M、N、D四点能够成平行四边形,此时点D在BC上,且BD=
s时,A、M、N、D四点能够成平行四边形,此时点D在BC上,且BD=![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】近几年购物的支付方式日益增多,某数学兴趣小组就此进行了抽样调查.调查结果显示,支付方式有:A微信、B支付宝、C现金、D其他,该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.

请你根据统计图提供的信息,解答下列问题:
(1)本次一共调查了多少名购买者?
(2)请补全条形统计图;在扇形统计图中A种支付方式所对应的圆心角为 度.
(3)若该超市这一周内有1600名购买者,请你估计使用A和B两种支付方式的购买者共有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H,∠K﹣∠H=27°,则∠K=( )
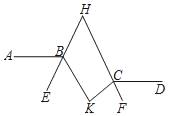
A. 76° B. 78° C. 80° D. 82°
查看答案和解析>>
科目:初中数学 来源: 题型:
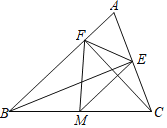
【题目】如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点,BC=10.
(1)若∠ABC=50°,∠ACB=60°,求∠EMF的度数;
(2)若EF=4,求△MEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
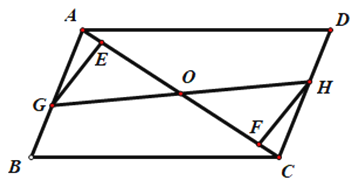
【题目】如图,在平行四边形ABCD中,点E、F在AC上,且AF=CE,点G、H分别在AB、CD上,且AG=CH,AC与GH相交于点O.
(1)求证:EG//FH;
(2)GH、EF互相平分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】顺次连接四边形ABCD四边中点得到新的四边形为菱形,那么原四边形ABCD为( )
A. 矩形
B. 菱形
C. 对角线相等的四边形
D. 对角线垂直的四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个口袋中放有290个涂有红、黑、白三种色的质地相同的小球,若红球个数是黑球个数的2倍多3个,从袋中任取一个球是白球的概率是![]() .
.
(1)求袋中红球的个数.
(2)求从袋中任取一个球是黑球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了庆祝校园艺术节,准备购买一批盆花布置校园.已知1盆A种花和2盆B种花一共需13元,2盆A种花和1盆B种花一共需11元.
(1)求1盆A种花和1盒B种花的售价各是多少元?
(2)学校准备购进这两种盆花共100盆,并且A种盆花的数量不超过B种盆花数量的2倍,请求出A种盆花的数量最多是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有四个三角形,分别满足下列条件:(1)一个角等于另外两个内角之和;(2)三个内角之比为3:4:5;(3)三边之比为5:12:13;(4)三边长分别为5,24,25.其中直角三角形有( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com