
【题目】如图,在平面直角坐标系中,点A的坐标为(m,m),点B的坐标为(n,﹣n),抛物线经过A、O、B三点,连接OA、OB、AB,线段AB交y轴于点C.已知实数m、n(m<n)分别是方程x2﹣2x﹣3=0的两根.
(1)求抛物线的解析式;
(2)若点P为线段OB上的一个动点(不与点O、B重合),直线PC与抛物线交于D、E两点(点D在y轴右侧),连接OD、BD.
①当△OPC为等腰三角形时,求点P的坐标;
②求△BOD 面积的最大值,并写出此时点D的坐标.

【答案】(1)y=![]() x2+
x2+![]() x;(2)①P点坐标为P1(
x;(2)①P点坐标为P1(![]() ,-
,-![]() )或P2(
)或P2(![]() ,﹣
,﹣![]() )或P3(
)或P3(![]() ,﹣
,﹣![]() ),②D(
),②D(![]() ,﹣
,﹣![]() ).
).
【解析】试题分析:(1)首先解方程得出A,B两点的坐标,进而利用待定系数法求出二次函数解析式即可;
(2)①首先求出AB的直线解析式,以及BO解析式,再利用等腰三角形的性质得出当OC=OP时,当OP=PC时,点P在线段OC的中垂线上,当OC=PC时分别求出x的值即可;
②利用S△BOD=S△ODQ+S△BDQ得出关于x的二次函数,进而得出最值即可.
试题解析:解(1)解方程x2﹣2x﹣3=0,
得 x1=3,x2=﹣1.
∵m<n,
∴m=﹣1,n=3
∴A(﹣1,﹣1),B(3,﹣3).
∵抛物线过原点,设抛物线的解析式为y=ax2+bx(a≠0).
∴![]() ,
,
解得: 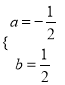 ,
,
∴抛物线的解析式为y=![]() x2+
x2+![]() x .
x .
(2)①设直线AB的解析式为y=kx+b.
∴![]() ;解得:
;解得: 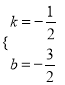 ,
,
∴直线AB的解析式为y=![]() x+
x+![]() .
.
∴C点坐标为(0,-![]() ).
).
∵直线OB过点O(0,0),B(3,﹣3),
∴直线OB的解析式为y=﹣x.
∵△OPC为等腰三角形,
∴OC=OP或OP=PC或OC=PC.
设P(x,﹣x),
(i)当OC=OP时,x2+(-x)2=![]() .
.
解得x1=![]() ,x2=-
,x2=-![]() ,(舍去).
,(舍去).
∴P1(![]() ,-
,-![]() ).
).
(ii)当OP=PC时,点P在线段OC的中垂线上,
∴P2(![]() ,﹣
,﹣![]() ).
).
(iii)当OC=PC时,由x2+(-x+![]() )2=
)2=![]() ,
,
解得x1=![]() ,x2=0(舍去).
,x2=0(舍去).
∴P3(![]() ,﹣
,﹣![]() ).
).
∴P点坐标为P1(![]() ,-
,-![]() )或P2(
)或P2(![]() ,﹣
,﹣![]() )或P3(
)或P3(![]() ,﹣
,﹣![]() ).
).
②过点D作DG⊥x轴,垂足为G,交OB于Q,过B作BH⊥x轴,垂足为H.
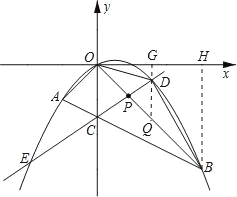
设Q(x,﹣x),D(x,-![]() x2+
x2+![]() x).
x).
S△BOD=S△ODQ+S△BDQ=![]() DQOG+
DQOG+![]() DQGH,
DQGH,
=![]() DQ(OG+GH),
DQ(OG+GH),
=![]() [x+(
[x+(![]() +
+ ![]() )]×3,
)]×3,
=-![]() (x-
(x-![]() )2+
)2+![]() ,
,
∵0<x<3,
∴当x=![]() 时,S取得最大值为
时,S取得最大值为![]() ,此时D(
,此时D(![]() ,﹣
,﹣![]() ).
).


科目:初中数学 来源: 题型:
【题目】某修理厂需要购进甲、乙两种配件,经调查,每个甲种配件的价格比每个乙种配件的价格少0.4万元,且用16万元购买的甲种配件的数量与用24万元购买的乙种配件的数量相同.
(1)求每个甲种配件、每个乙种配件的价格分别为多少万元;
(2)现投入资金80万元,根据维修需要预测,甲种配件要比乙种配件至少要多22件,问乙种配件最多可购买多少件.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嘉淇乘坐一艘游船出海游玩,游船上的雷达扫描探测得到的结果如图所示,每相邻两个圆之间距离是1km (最小圆的半径是1km ),下列关于小艇 A , B 的位置描述,正确的是( )

A.小艇 A 在游船的北偏东60°方向上,且与游船的距离是3km
B.游船在小艇 A 的南偏西60°方向上,且与小艇 A 的距离是3km
C.小艇 B 在游船的北偏西30°方向上,且与游船的距离是 2km
D.游船在小艇 B 的南偏东60°方向上,且与小艇 B 的距离是 2km
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市环保局决定购买A、B两种型号的扫地车共40辆,对城区所有公路地面进行清扫.已知1辆A型扫地车和2辆B型扫地车每周可以处理地面垃圾100吨,2辆A型扫地车和1辆B型扫地车每周可以处理垃圾110吨.
(1)求A、B两种型号的扫地车每辆每周分别可以处理垃圾多少吨?
(2)已知A型扫地车每辆价格为25万元,B型扫地车每辆价格为20万元,要想使环保局购买扫地车的资金不超过910万元,但每周处理垃圾的量又不低于1400吨,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少资金是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式,探究其中规律.
第1个等式:![]() ;
;
第2个等式:![]()
第3个等式:![]()
……
(1)第4个等式:![]() (直接填写结果);
(直接填写结果);
(2)根据以上规律请计算:![]() ;
;
(3)通过以上规律请猜想写出:![]() (直接填写结果).
(直接填写结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级社会实践小组去某商场调查商品的销售情况,了解到该商场以每件80元的价格购进了某品牌衬衫500件,并以每件120元的价格销售了400件,商场准备采取促销措施,将剩下的衬衫降价销售.
(1)每件衬衫降价多少元时,销售完这批衬衫正好达到盈利45%的预期目标?
(2)在(1)的条件下,某公司给员工发福利,在该商场促销钱购买了20件该品牌的衬衫发给员工,后因为有新员工加入,又要购买5件该衬衫,购买这5件衬衫时恰好赶上该商场进行促销活动,求该公司购买这25件衬衫的平均价格.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,点
,点![]() 分别在射线
分别在射线![]() 上运动(不与点
上运动(不与点![]() 重合)
重合)
观察:
(1)如图1,若![]() 和
和![]() 的平分线交于点
的平分线交于点![]() ,
,![]() _____°
_____°

猜想:
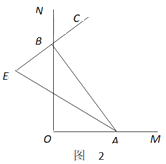
(2)如图2,随着点![]() 分别在射线
分别在射线![]() 上运动(不与点
上运动(不与点![]() 重合). 若
重合). 若![]() 是
是![]() 的平分线,
的平分线,![]() 的反向延长线与
的反向延长线与![]() 的平分线交于点
的平分线交于点![]() ,
, ![]() 的大小会变吗?如果不会,求
的大小会变吗?如果不会,求![]() 的度数;如果会改变,说明理由.
的度数;如果会改变,说明理由.
拓展:
(3)如图3,在(2)基础上,小明将![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在四边形
落在四边形![]() 内点
内点![]() ′的位置,求
′的位置,求![]() 的度数.
的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人相约元旦登山,甲、乙两人距地面的高度y(m)与登山时间x(min)之间的函数图像如图所示,根据图像所提供的信息解答下列问题:
(1)t= min.
(2)若乙提速后,乙登山的上升速度是甲登山的上升速度3倍,
①则甲登山的的上升速度是 m/min;
②请求出甲登山过程中,距地面的高度y(m)与登山时间x(min)之间的函数关系式.
③当甲、乙两人距地面高度差为70m时,求x的值(直接写出满足条件的x值).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com