
【题目】某市环保局决定购买A、B两种型号的扫地车共40辆,对城区所有公路地面进行清扫.已知1辆A型扫地车和2辆B型扫地车每周可以处理地面垃圾100吨,2辆A型扫地车和1辆B型扫地车每周可以处理垃圾110吨.
(1)求A、B两种型号的扫地车每辆每周分别可以处理垃圾多少吨?
(2)已知A型扫地车每辆价格为25万元,B型扫地车每辆价格为20万元,要想使环保局购买扫地车的资金不超过910万元,但每周处理垃圾的量又不低于1400吨,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少资金是多少?
【答案】(1)40,30;(2)购买方案见解析,方案一所需资金最少,900万元.
【解析】
(1)根据题意列出二元一次方程组即可解题,(2)设购买A型扫地车m辆,B型扫地车(40﹣m)辆,所需资金为y元,根据题意建立一元一次不等式组求出所有满足条件的方案,再表示出总资金y=5m+800,根据一次函数的单调性即可确定所选方案,求最少资金..
解:(1)设A、B两种型号的扫地车每辆每周分别可以处理垃圾a吨、b吨,
![]() ,
,
解得:![]() ,
,
答:(1)求A、B两种型号的扫地车每辆每周分别可以处理垃圾40吨,30吨;
(2)设购买A型扫地车m辆,B型扫地车(40﹣m)辆,所需资金为y元,
![]() ,解得,20≤m≤22,
,解得,20≤m≤22,
∵m为整数,
∴m=20,21,22,
∴共有三种购买方案,
方案一:购买A型扫地车20辆,B型扫地车20辆;
方案二:购买A型扫地车21辆,B型扫地车19辆;
方案三:购买A型扫地车22辆,B型扫地车18辆;
∵y=25m+20(40﹣m)=5m+800,k=5![]() 0,
0,
∴y随着x的增大而增大,
∴当m=20时,y取得最小值,此时y=900,
答:方案一:购买A型扫地车20辆,B型扫地车20辆所需资金最少,最少资金是900万元.


 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:
【题目】已知点E(x0,y0),F(x2,y2),点M(x1,y1)是线段EF的中点,则![]() ,
, ![]() .在平面直角坐标系中有三个点A(1,-1),B(-1,-1),C(0,1),点P(0,2)关于A的对称点为P1(即P,A,P1三点共线,且PA=P1A),P1关于B的对称点为P2,P2关于C的对称点为P3,按此规律继续以A,B,C为对称点重复前面的操作,依次得到P4,P5,P6,…,则点P2015的坐标是( )
.在平面直角坐标系中有三个点A(1,-1),B(-1,-1),C(0,1),点P(0,2)关于A的对称点为P1(即P,A,P1三点共线,且PA=P1A),P1关于B的对称点为P2,P2关于C的对称点为P3,按此规律继续以A,B,C为对称点重复前面的操作,依次得到P4,P5,P6,…,则点P2015的坐标是( )
A. (0,0) B. (0,2)
C. (2,-4) D. (-4,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王师傅有一根长![]() 的钢材,他想将这段钢材锯断后焊成三个面积分别为
的钢材,他想将这段钢材锯断后焊成三个面积分别为![]() ,
,![]() ,
,![]() 的正方形铁框,如图.问王师傅的钢材够用吗?请通过计算说明理由.(参考数据:
的正方形铁框,如图.问王师傅的钢材够用吗?请通过计算说明理由.(参考数据:![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,按如下步骤作图: ①分别以点B、C为圆心,大于 ![]() AB的长为半径作弧,两弧相交于点M和N;
AB的长为半径作弧,两弧相交于点M和N;
②作直线MN交AC于点D,
③连接BD,
若AC=8,则BD的长为 . 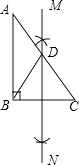
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】花园内有一块边长为a的正方形土地,园艺师设计了三种不同的图案,如图①②③所示,其中的阴影部分用于种植花草,试比较三种方案中用于种植花草部分的面积的大小,并用平移的知识说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】湖州素有鱼米之乡之称,某水产养殖大户为了更好地发挥技术优势,一次性收购了 ![]()
![]() 淡水鱼,计划养殖一段时间后再出售.已知每天放养的费用相同,放养
淡水鱼,计划养殖一段时间后再出售.已知每天放养的费用相同,放养 ![]() 天的总成本为
天的总成本为 ![]() 万元;放养
万元;放养 ![]() 天的总成本为
天的总成本为 ![]() 万元(总成本=放养总费用+收购成本).
万元(总成本=放养总费用+收购成本).
(1)设每天的放养费用是 ![]() 万元,收购成本为
万元,收购成本为 ![]() 万元,求
万元,求 ![]() 和
和 ![]() 的值;
的值;
(2)设这批淡水鱼放养 ![]() 天后的质量为
天后的质量为 ![]() (
( ![]() ),销售单价为
),销售单价为 ![]() 元/
元/ ![]() .根据以往经验可知:
.根据以往经验可知: ![]() 与
与 ![]() 的函数关系为
的函数关系为 ![]() ;
; ![]() 与
与 ![]() 的函数关系如图所示.
的函数关系如图所示.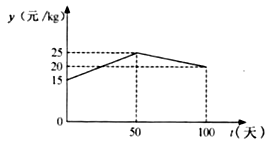
①分别求出当 ![]() 和
和 ![]() 时,
时, ![]() 与
与 ![]() 的函数关系式;
的函数关系式;
②设将这批淡水鱼放养 ![]() 天后一次性出售所得利润为
天后一次性出售所得利润为 ![]() 元,求当
元,求当 ![]() 为何值时,
为何值时, ![]() 最大?并求出最大值.(利润=销售总额-总成本)
最大?并求出最大值.(利润=销售总额-总成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1∥l2,直线l与l1、l2分别交于A、B两点,点M、N分别在l1、l2上,点M、N、P均在l的同侧(点P不在l1、l2上),若∠PAM=α,∠PBN=β.
(1)当点P在l1与l2之间时.
①求∠APB的大小(用含α、β的代数式表示);
②若∠PAM的平分线与∠PBN的平分线交于点P1,∠P1AM的平分线与∠P1BN的平分线交于点P2,…,∠Pn﹣1AM的平分线与∠Pn﹣1BN的平分线交于点Pn,则∠AP1B= ,∠APnB= .(用含α、β的代数式表示,其中n为正整数)
(2)当点P不在l1与l2之间时.
若∠PAM的平分线与∠PBN的平分线交于点P,∠P1AM的平分线与∠P1BN的平分线交于点P2,…,∠Pn﹣1AM的平分线与∠Pn﹣1BN的平分线交于点Pn,请直接写出∠APnB的大小.(用含α、β的代数式表示,其中n为正整数)
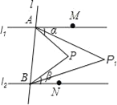
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com