
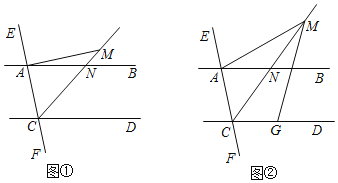
【题目】直线AB∥CD,直线EF分别交AB、CD于点A、C,CM是∠ACD的平分线,CM交AB于点N.
(1)如图①,过点A作AC的垂线交CM于点M,若∠MCD=55°,求∠MAN的度数;
(2)如图②,点G是CD上的一点,连接MA、MG,若MC平分∠AMG且∠AMG=36°,∠MGD+∠EAB=180°,求∠ACD的度数.

【答案】(1)∠MAN=20°;(2)∠ACD=108°.
【解析】
(1)依据角平分线的定义以及平行线的性质,即可得到∠BAC的度数,再根据垂线的定义,即可得出∠MAN的度数;
(2)设∠ACD=α,根据角平分线以及平行线即可得到∠MCG=![]() ,ACD=
,ACD=![]() α,∠BAC=∠MGD=180°-α,依据三角形外角性质,即可得到α的度数.
α,∠BAC=∠MGD=180°-α,依据三角形外角性质,即可得到α的度数.
(1)∵CM是∠ACD的平分线,∠MCD=55°,
∴∠ACD=2∠MCD=110°,
又∵AB∥CD,
∴∠BAC=180°﹣110°=70°,
又∵AM⊥EF,
∴∠MAN=90°﹣70°=20°;
(2)∵MC平分∠AMG且∠AMG=36°,
∴∠CMG=18°,
∵MC平分∠ACG,
∴∠MCG=![]() ∠ACG,
∠ACG,
∵∠CAB+∠EAB=180°,∠MGD+∠EAB=180°,
∴∠BAC=∠MGD,
∵AB∥CD,
∴∠BAC+∠ACD=180°,
设∠ACD=α,则∠MCG=![]() ACD=
ACD=![]() α,∠BAC=∠MGD=180°﹣α,
α,∠BAC=∠MGD=180°﹣α,
∵∠MGD是△CMG的外角,
∴∠MGD=∠CMG+∠MCG,即180°﹣α=![]() α+18°,
α+18°,
解得α=108°,
∴∠ACD=108°.


科目:初中数学 来源: 题型:
【题目】一个口袋中放有290个涂有红、黑、白三种色的质地相同的小球,若红球个数是黑球个数的2倍多3个,从袋中任取一个球是白球的概率是![]() .
.
(1)求袋中红球的个数.
(2)求从袋中任取一个球是黑球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店用6000元购进A,B两种新式服装,按标价售出后可获得毛利润3800元(毛利润=售价-进价).这两种服装的进价,标价如表所示.
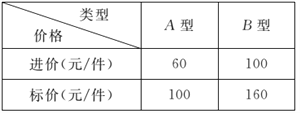
(1)求这两种服装各购进的件数;
(2)如果A种服装按标价的8折出售,B种服装按标价的7折出售,那么这批服装全部售完后,服装店比按标价出售少收入多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有四个三角形,分别满足下列条件:(1)一个角等于另外两个内角之和;(2)三个内角之比为3:4:5;(3)三边之比为5:12:13;(4)三边长分别为5,24,25.其中直角三角形有( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
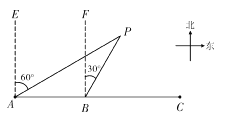
【题目】如图所示,C城市在A城市正东方向,现计划在A,C两城市间修建一条高速铁路(即线段AC),经测量,森林保护区的中心P在城市A的北偏东60°方向上,在线段AC上距A城市120 km的B处测得P在北偏东30°方向上,已知森林保护区是以点P为圆心,100 km为半径的圆形区域,请问计划修建的这条高速铁路是否穿越保护区,为什么?(参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=90°,P是BC上一点,且DB=DC,过BC上一点P,作PE⊥AB于E,PF⊥DC于F,已知:AD:DB=1:3,BC=![]() ,则PE+PF的长是( )
,则PE+PF的长是( )

A. ![]() B. 6C.
B. 6C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如下表:


(1)当桌子上放有x(个)碟子时,请写出此时碟子的高度(用含x的式子表示);
(2)分别从三个方向上看,其三视图如上图所示,厨房师傅想把它们整齐叠成一摞,求叠成一摞后的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
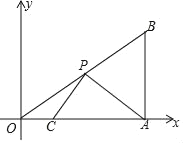
【题目】在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上,顶点B的坐标为(3,![]() ),点C的坐标为(1,0),点P为斜边OB上的一动点,则PA+PC的最小值_____.
),点C的坐标为(1,0),点P为斜边OB上的一动点,则PA+PC的最小值_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
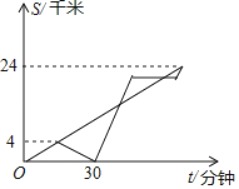
【题目】在网红重庆,磁器口和洪崖洞是外地游客必到的打卡景点.现有一自行车队计划从磁器口到洪崖洞出发一段时间后,发现有贵重物品落在了磁器口,于是安排小南骑自行车以原速返回,剩下的成员速度不变向洪崖洞前进,小南取回物品后,改乘出租车追赶车队(取物品、等车时间忽略不计),小南在追赶上自行车队后仍乘坐出租车,再行驶10分钟后遭遇堵车,在此期间,自行车队反超出租车,拥堵30分钟后交通恢复正常,出租车以原速开往洪崖洞,最终出租车和自行车队同时到达,设自行车队和小南行驶时间为t(分钟),与磁器口距离s(千米),s与t的函数关系如图所示,则在第二次相遇后,出租车还经过了_____分钟到达洪崖洞.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com