
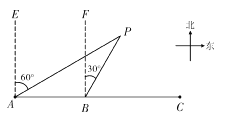
【题目】如图所示,C城市在A城市正东方向,现计划在A,C两城市间修建一条高速铁路(即线段AC),经测量,森林保护区的中心P在城市A的北偏东60°方向上,在线段AC上距A城市120 km的B处测得P在北偏东30°方向上,已知森林保护区是以点P为圆心,100 km为半径的圆形区域,请问计划修建的这条高速铁路是否穿越保护区,为什么?(参考数据:![]() )
)
科目:初中数学 来源: 题型:
【题目】如图,某校一幢教学大楼的顶部竖有一块“传承文明,启智求真”的宣传牌CD.小明在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度i=1:![]() ,AB=10米,AE=15米,求这块宣传牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据:
,AB=10米,AE=15米,求这块宣传牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y=![]() 的图象上.若点B在反比例函数y=
的图象上.若点B在反比例函数y=![]() 的图象上,则k的值为( )
的图象上,则k的值为( )

A.-4 B.4 C.-2 D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AC、BD交于点O,AD=15,AO=12.动点P以每秒2个单位的速度从点A出发,沿AC向点C匀速运动.同时,动点Q以每秒1个单位的速度从点D出发,沿DB向点B匀速运动.当其中有一点列达终点时,另一点也停止运动,设运动的时间为t秒.
(1)求线段DO的长;
(2)设运动过程中△POQ两直角边的和为y,请求出y关于x的函数解析式;
(3)请直接写出点P在线段OC上,点Q在线段DO上运动时,△POQ面积的最大值,并写出此时的t值.

查看答案和解析>>
科目:初中数学 来源: 题型:
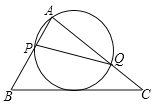
【题目】如图,在△ABC中,已知AB=5,BC=8,AC=7,动点P、Q分别在边AB、AC上,使△APQ的外接圆与BC相切,则线段PQ的最小值等于_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线AB∥CD,直线EF分别交AB、CD于点A、C,CM是∠ACD的平分线,CM交AB于点N.
(1)如图①,过点A作AC的垂线交CM于点M,若∠MCD=55°,求∠MAN的度数;
(2)如图②,点G是CD上的一点,连接MA、MG,若MC平分∠AMG且∠AMG=36°,∠MGD+∠EAB=180°,求∠ACD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一张三角形纸片ABC(如图甲),其中AB=AC.将纸片沿过点B的直线折叠,使点C落到AB边上的E点处,折痕为BD(如图乙).再将纸片沿过点E的直线折叠,点A恰好与点D重合,折痕为EF(如图丙).原三角形纸片ABC中,∠ABC的大小为______°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),四边形ABCD中,AB∥CD,∠ADC=90°,P从A点出发,以每秒1个单位长度的速度,按A→B→C→D的顺序在边上匀速运动,设P点的运动时间为t秒,△PAD的面积为S,S关于t的函数图象如图(2)所示,当P运动到BC中点时,△PAD的面积为( )
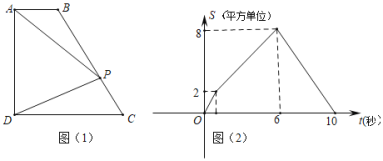
A. 4B. 5C. 6D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工厂加工某种茶叶,计划一周生产![]() 千克,平均每天生产
千克,平均每天生产![]() 千克,由于各种原因实际每天产量与计划量相比有出入,某周七天的生产情况记录如下(超产为正、减产为负):
千克,由于各种原因实际每天产量与计划量相比有出入,某周七天的生产情况记录如下(超产为正、减产为负):
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(![]() )这一周的实际产量是多少千克?
)这一周的实际产量是多少千克?
(![]() )该厂规定工人工资参照平均产量计发,每千克
)该厂规定工人工资参照平均产量计发,每千克![]() 元.若超产,则超产的部分每千克
元.若超产,则超产的部分每千克![]() 元;若低于平均产量,按实际产量计发,而且每少
元;若低于平均产量,按实际产量计发,而且每少![]() 千克扣除
千克扣除![]() 元,那么该工厂工人这一周的工资总额是多少?
元,那么该工厂工人这一周的工资总额是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com