
【题目】如图,在△ABC中,已知AB=5,BC=8,AC=7,动点P、Q分别在边AB、AC上,使△APQ的外接圆与BC相切,则线段PQ的最小值等于_______________.
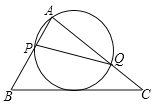
【答案】![]()
【解析】如图,设点O是△APQ的外接圆的圆心,连接OP,OQ,作OH⊥PQ于点H,过点A作AD⊥BC于点D,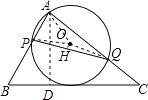
∴PH=QH=![]() PQ,
PQ,
∵OP=OQ,
∴∠POH=![]() ∠POQ,
∠POQ,
∵∠POQ=2∠BAC,
∴∠POH=∠BAC,
在Rt△POH中,PH=OPsin∠POH=OAsin∠BAC,
∴PQ=2OAsin∠BAC,
即当OA最小时,PQ最小,
∵当AD是直径时,即OA=![]() AD时,PQ最小,
AD时,PQ最小,
设BD=x,则CD=8-x,
∵在Rt△ABD中,AD2=AB2-AD2,
在Rt△ACD中,AD2=AC2-CD2,
∴25-x2=49-(8-x)2,
解得:x=![]() ,
,
∴AD=![]() =
=![]() ,
,
∴OA=![]() ,
,
设AC边上的高为h,
则ACh=BCAD,
∴h=![]() ,
,
∴sin∠BAC=![]() =
=![]() ,
,
∴PQ=2OAsin∠BAC=2×![]() ×
×![]() =
=![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】平行四边形ABCD中,E,F是对角线BD上的两点, 如果添加一个条件使△ABE≌△CDF,则添加的条件不能是( )

A. AE=CF B. BE=FD C. BF=DE D. ∠1=∠2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠A+∠D=180°,∠1=3∠2,∠2=24°,点P是BC上的一点.
(1)请写出图中∠1的一对同位角,一对内错角,一对同旁内角;
(2)求∠EFC与∠E的度数;
(3)若∠BFP=46°,请判断CE与PF是否平行?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图中的小方格都是边长为1的正方形, △ABC与△A′ B′ C′是关于点0为位似中心的位似图形,它们的顶点都在小正方形的顶点上.

(1)画出位似中心点0;
(2)求出△ABC与△A′B′C′的位似比;
(3)以点0为位似中心,再画一个△A1B1C1,使它与△ABC的位似比等于1.5.
查看答案和解析>>
科目:初中数学 来源: 题型:
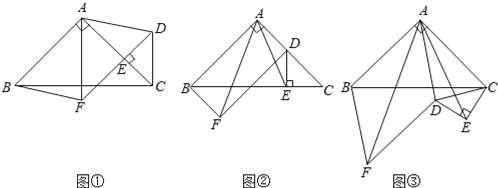
【题目】如图①,在等腰Rt△ABC中,∠BAC=90°,点E在AC上(且不与点A、C重合),在△ABC的外部作等腰Rt△CED,使∠CED=90°,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)请直接写出线段AF,AE的数量关系;
(2)①将△CED绕点C逆时针旋转,当点E在线段BC上时,如图②,连接AE,请判断线段AF,AE的数量关系,并证明你的结论;
②若AB=2![]() ,CE=2,在图②的基础上将△CED绕点C继续逆时针旋转一周的过程中,当平行四边形ABFD为菱形时,直接写出线段AE的长度.
,CE=2,在图②的基础上将△CED绕点C继续逆时针旋转一周的过程中,当平行四边形ABFD为菱形时,直接写出线段AE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
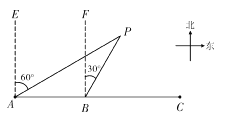
【题目】如图所示,C城市在A城市正东方向,现计划在A,C两城市间修建一条高速铁路(即线段AC),经测量,森林保护区的中心P在城市A的北偏东60°方向上,在线段AC上距A城市120 km的B处测得P在北偏东30°方向上,已知森林保护区是以点P为圆心,100 km为半径的圆形区域,请问计划修建的这条高速铁路是否穿越保护区,为什么?(参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△DAC、△EBC均是等边三角形,点A、C、B在同一条直线上,且AE、BD分别与CD、CE交于点M、N.

求证:(1)AE=DB;
(2)△CMN为等边三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“珍重生命,注意安全!”同学们在上下学途中一定要注意骑车安全.小明骑单车上学,当他骑了一段时,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校,以下是他本次所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是多少米;
(2)小明在书店停留了多少分钟;
(3)本次上学途中,小明一共行驶了多少米?一共用了多少分钟?
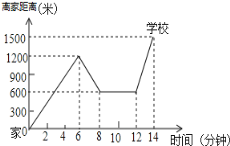
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司研发1000件新产品,需要精加工后才能投放市场.现在甲、乙两个工厂加工这批产品,已知甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天,而乙工厂每天加工的件数是甲工厂每天加工件数的1.25倍,公司需付甲工厂加工费用每天100元,乙工厂加工费用每天125元.
(1)甲、乙两个工厂每天各能加工多少件新产品?
(2)两个工厂同时合作完成这批产品,共付加工费多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com