
【题目】已知:如图,△DAC、△EBC均是等边三角形,点A、C、B在同一条直线上,且AE、BD分别与CD、CE交于点M、N.

求证:(1)AE=DB;
(2)△CMN为等边三角形.
【答案】证明略
【解析】
证明:(1)∵△DAC、△EBC均是等边三角形,
∴AC=DC,EC=BC,∠ACD=∠BCE=60°,………… 2分
∴∠ACD+∠DCE=∠BCE+∠DCE,
即∠ACE=∠DCB. ……………… 3分
在△ACE和△DCB中,
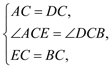
∴△ACE≌△DCB(SAS). ………… 5分
∴AE=DB. ……………… 6分
(2)由(1)可知:△ACE≌△DCB,
∴∠CAE=∠CDB,
即∠CAM=∠CDN. ……………… 7分
∵△DAC、△EBC均是等边三角形,
∴AC=DC,∠ACM=∠BCE=60°.
又点A、C、B在同一条直线上,
∴∠DCE=180°-∠ACD-∠BCE=180°-60°-60°=60°,
即∠DCN=60°.
∴∠ACM=∠DCN. ………… 8分
在△ACM和△DCN中,
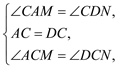
∴△ACM≌△DCN(ASA). ……………… 10分
∴CM=CN. ……………… 11分
又∠DCN=60°,
∴△CMN为等边三角形. ……………12分


科目:初中数学 来源: 题型:
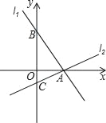
【题目】如图,过点A(2,0)的两条直线l1、l2分别交y轴于点B、C,其中点B在原点上方,点C在原点下方,已知AB=![]() .
.
(1)求点B的坐标;
(2)若OC:OB=1:3,求直线l2的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
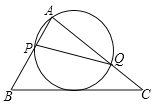
【题目】如图,在△ABC中,已知AB=5,BC=8,AC=7,动点P、Q分别在边AB、AC上,使△APQ的外接圆与BC相切,则线段PQ的最小值等于_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
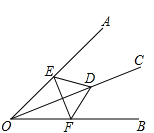
【题目】如图,已知射线OC上的任意一点到∠AOB的两边的距离都相等,点D、E、F分别为边OC、OA、OB上,如果要想证得OE=OF,只需要添加以下四个条件中的某一个即可,请写出所有可能的条件的序号__________.
①∠ODE=∠ODF;②∠OED=∠OFD;③ED=FD;④EF⊥OC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一张三角形纸片ABC(如图甲),其中AB=AC.将纸片沿过点B的直线折叠,使点C落到AB边上的E点处,折痕为BD(如图乙).再将纸片沿过点E的直线折叠,点A恰好与点D重合,折痕为EF(如图丙).原三角形纸片ABC中,∠ABC的大小为______°.

查看答案和解析>>
科目:初中数学 来源: 题型:
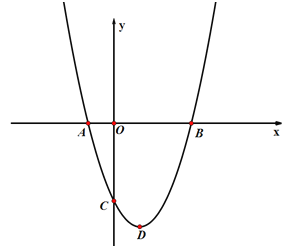
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于A、B两点(点A在点B的左侧),点B的坐标为(3,0),与
轴交于A、B两点(点A在点B的左侧),点B的坐标为(3,0),与![]() 轴交于点C(0,-3),顶点为D.
轴交于点C(0,-3),顶点为D.
(1)求抛物线的解析式及顶点D的坐标.
(2)联结AC,BC,求∠ACB的正切值.
(3)点P是x轴上一点,是否存在点P使得△PBD与△CAB相似,若存在,请求出点P的坐标;若不存在,请说明理由.
(4)M是抛物线上一点,点N在![]() 轴,是否存在点N,使得以点A,C,M,N为顶点的四边形是平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
轴,是否存在点N,使得以点A,C,M,N为顶点的四边形是平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,排球运动员站在点![]() 处练习发球,将球从
处练习发球,将球从![]() 点正上方
点正上方![]() 的
的![]() 处发出,把球看成点,其运行的高度
处发出,把球看成点,其运行的高度![]() 与运行的水平距离
与运行的水平距离![]() 满足关系式
满足关系式![]() .已知球网与
.已知球网与![]() 点的水平距离为
点的水平距离为![]() ,高度为
,高度为![]() ,球场的边界距
,球场的边界距![]() 点的水平距离为
点的水平距离为![]() .
.
(![]() )求
)求![]() 与
与![]() 的关系式(不要求写出自变量
的关系式(不要求写出自变量![]() 的取值范围).
的取值范围).
(![]() )球能否越过球网?球会不会出界?请说明理由.
)球能否越过球网?球会不会出界?请说明理由.
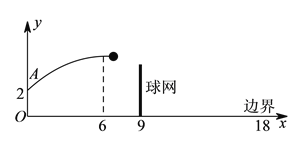
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:△ABC的周长为30cm,把△ABC的边AC对折,使顶点C和点A重合,折痕交BC边于点D,交AC边与点E,连接AD,若AE=4cm,则△ABD的周长是( )

A. 22cmB. 20cmC. 18cmD. 15cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com