
【题目】一个平行四边形的一条边长为5,两条对角线的长分别为6和8,则它的面积为________.
【答案】24
【解析】
由题意画出相应的图形,得到平行四边形的边BC=5,对角线AC和BD分别为6和8,根据平行四边形的对角线互相平分,求出OB及OC的长,计算发现OC2+OB2=BC2,利用勾股定理的逆定理得到∠BOC为直角,根据垂直定义得到AC与BD垂直,继而得到四边形ABCD为菱形,再根据菱形的面积等于对角线乘积的一半进行求解即可.
根据题意画出相应的图形,如图所示:
则有平行四边形ABCD中,BC=5,AC=6,BD=8,
∴OC=![]() AC=3,OB=
AC=3,OB=![]() BD=4,
BD=4,
∵OC2+OB2=9+16=25,BC2=25,
∴OC2+OB2=BC2,
∴∠BOC=90°,即AC⊥BD,
∴四边形ABCD为菱形,
则菱形ABCD的面积S=![]() ACBD=
ACBD=![]() ×6×8=24,
×6×8=24,
故答案为:24.



科目:初中数学 来源: 题型:
【题目】甲、乙两工程队合作完成一项工程,需要12天完成,工程费用共36000元,若甲、乙两工程队单独完成此项工程,乙工程队所用的时间是甲工程队的1.5倍,乙工程队每天的费用比甲工程队少800元.
(1)问甲、乙两工程队单独完成此项工程各需多少天?
(2)若让一个工程队单独完成这项工程,哪个工程队的费用较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小组在“用频率估计概率”的实验中,统计了某种频率结果出现的频率,绘制了如图所示的折线统计图,那么符合这一结果的实验最有可能的是( )

A. 掷一枚质地均匀的硬币,落地时结果是“正面向上”
B. 掷一个质地均匀的正六面体骰子,落地时朝上的面点数是6
C. 在“石头剪刀、和”的游戏中,小明随机出的是“剪刀”
D. 袋子中有1个红球和2个黄球,只有颜色上的区别,从中随机取出一个球是黄球
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平行四边形ABCD中,E,F是对角线BD上的两点, 如果添加一个条件使△ABE≌△CDF,则添加的条件不能是( )

A. AE=CF B. BE=FD C. BF=DE D. ∠1=∠2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=1,BC=2,则△ABE和△BC′F的周长之和为( )

A. 3 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
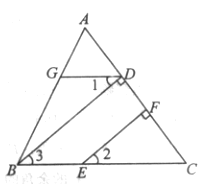
【题目】如图,已知BD⊥AC,EF⊥AC,垂足分别为D、F,∠1=∠2,请将证明∠ADG=∠C过程填写完整.
证明:BD⊥AC,EF⊥AC(已知)
∴∠BDC=∠EFC=90°
∴BD∥
∠2=∠3
又∵∠1=∠2(已知)
∴∠1=∠3(等量代换)
∴DG∥
∴∠ADG=∠C
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠ABC的平分线交CD于点E.
(1)若∠A=70°,求∠ABE的度数;
(2)若AB∥CD,且∠1=∠2,判断DF和BE是否平行,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠A+∠D=180°,∠1=3∠2,∠2=24°,点P是BC上的一点.
(1)请写出图中∠1的一对同位角,一对内错角,一对同旁内角;
(2)求∠EFC与∠E的度数;
(3)若∠BFP=46°,请判断CE与PF是否平行?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△DAC、△EBC均是等边三角形,点A、C、B在同一条直线上,且AE、BD分别与CD、CE交于点M、N.

求证:(1)AE=DB;
(2)△CMN为等边三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com