
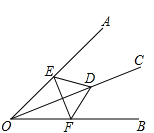
【题目】如图,已知射线OC上的任意一点到∠AOB的两边的距离都相等,点D、E、F分别为边OC、OA、OB上,如果要想证得OE=OF,只需要添加以下四个条件中的某一个即可,请写出所有可能的条件的序号__________.
①∠ODE=∠ODF;②∠OED=∠OFD;③ED=FD;④EF⊥OC.
 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=1,BC=2,则△ABE和△BC′F的周长之和为( )

A. 3 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系中,A(a,0),C(b,2),且满足(a+2)2+![]() =0,过C作CB⊥x轴于B.
=0,过C作CB⊥x轴于B.

(1)求三角形ABC的面积;
(2)如图②,若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,求∠AED的度数;
(3)在y轴上是否存在点P,使得三角形ACP和三角形ABC的面积相等?若存在,求出P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
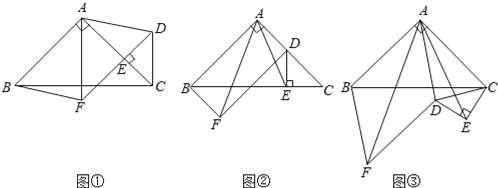
【题目】如图①,在等腰Rt△ABC中,∠BAC=90°,点E在AC上(且不与点A、C重合),在△ABC的外部作等腰Rt△CED,使∠CED=90°,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)请直接写出线段AF,AE的数量关系;
(2)①将△CED绕点C逆时针旋转,当点E在线段BC上时,如图②,连接AE,请判断线段AF,AE的数量关系,并证明你的结论;
②若AB=2![]() ,CE=2,在图②的基础上将△CED绕点C继续逆时针旋转一周的过程中,当平行四边形ABFD为菱形时,直接写出线段AE的长度.
,CE=2,在图②的基础上将△CED绕点C继续逆时针旋转一周的过程中,当平行四边形ABFD为菱形时,直接写出线段AE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
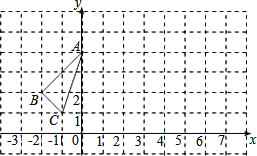
【题目】如图,已知在平面直角坐标系中,三角形ABC的位置如图所示.
(1)请写出A、B、C三点的坐标;
(2)求△ABC的面积;
(3)△ABC经过平移后得到△A′B′C′,已知△ABC内的任意一点P(x,y)在△A′B′C′内的对应点P′的坐标为(x+6,y+2).请你写出△A′B′C′各顶点的坐标并图中画出△A′B′C′.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△DAC、△EBC均是等边三角形,点A、C、B在同一条直线上,且AE、BD分别与CD、CE交于点M、N.

求证:(1)AE=DB;
(2)△CMN为等边三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,青少年中的近视眼和肥胖案例日趋增多,人们普遍意识到健康的身体是学习的保障,所以体育活动越来越受重视.某商店分两次购进跳绳和足球两种商品进行销售,每次购进同一种商品的进价相同,具体情况如下表所示.
购进数量(件) | 购进所需费用(元) | ||
跳绳 | 足球 | ||
第一次 | 30 | 40 | 3800 |
第二次 | 40 | 30 | 3200 |
(1)跳绳和足球两种商品每件的进价分别是多少元?
(2)商店计划用5300元的资金进行第三次进货,共购进跳绳和足球两种商品100件,其中要求足球的数量不少于跳绳的数量,有哪几种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了节约用水,对自来水的收费标准作如下规定:每月每户用水不超过10吨的部分,按2元/吨收费;超过10吨的部分按2.5元/吨收费.
(1)若黄老师家5月份用水16吨,问应交水费多少元?
(2)若黄老师家7月用水a吨,问应交水费多少元?(用a的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
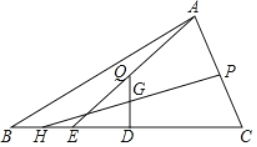
【题目】如图,在△ABC中,D为BC边中点,P为AC边中点,E为BC上一点且BE=![]() CE,连接AE,取AE中点Q并连接QD,取QD中点G,延长PG与BC边交于点H,若BC=6,则HE=_____.
CE,连接AE,取AE中点Q并连接QD,取QD中点G,延长PG与BC边交于点H,若BC=6,则HE=_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com