
【题目】如图,已知在平面直角坐标系中,三角形ABC的位置如图所示.
(1)请写出A、B、C三点的坐标;
(2)求△ABC的面积;
(3)△ABC经过平移后得到△A′B′C′,已知△ABC内的任意一点P(x,y)在△A′B′C′内的对应点P′的坐标为(x+6,y+2).请你写出△A′B′C′各顶点的坐标并图中画出△A′B′C′.
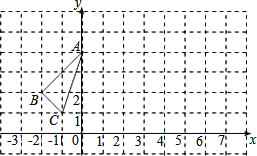
【答案】(1)点A的坐标为(0,4),点B的坐标为(﹣2,2),点C的坐标为(﹣1,1);(2)S△ABC=2;(3)A'坐标为(6,6),点B'的坐标为(4,4),点C'的坐标为(5,3);作出图形如图所示,见解析.
【解析】
(1)结合直角坐标系,即可得出A、B、C三点的坐标;
(2)根据图形可判断△ABC为直角三角形,∠ABC=90°,代入直角三角形的面积公式进行计算即可.
(3)平移是按照:向右平移6个单位,向上平移2个单位进行,从而可得出△A′B′C′各顶点的坐标,可也画出图形.
(1)结合图形可得:点A的坐标为(0,4),点B的坐标为(﹣2,2),点C的坐标为(﹣1,1);
(2)由图形可得∠ABC=90°,
则S△ABC=![]() AB×BC=
AB×BC=![]() ×2
×2![]() ×
×![]() =2;
=2;
(3)由点P平移前后的坐标可得:平移是按照:向右平移6个单位,向上平移2个单位进行的,
则A'坐标为(6,6),点B'的坐标为(4,4),点C'的坐标为(5,3);
作出图形如下所示:
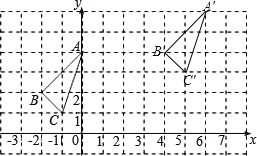 .
.


科目:初中数学 来源: 题型:
【题目】将若干枝铅笔分给甲、乙两个班级,甲班有一人分到6枝,其余的每人都分到13枝,乙班有一人分到5枝,其余的每人都分到10枝.如果分到两个班级的铅笔数目相同,并且大于100而不超过200那么甲、乙两个班各有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
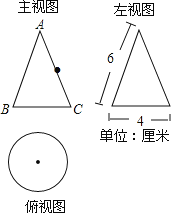
【题目】如图是一个几何体的三视图.
(1)写出该几何体的名称,并根据所示数据计算这个几何体的表面积;
(2)如果一只蚂蚁要从这个几何体中的点B出发,沿表面爬到AC的中点D,请你求出这个线路的最短路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
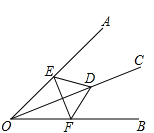
【题目】如图,已知射线OC上的任意一点到∠AOB的两边的距离都相等,点D、E、F分别为边OC、OA、OB上,如果要想证得OE=OF,只需要添加以下四个条件中的某一个即可,请写出所有可能的条件的序号__________.
①∠ODE=∠ODF;②∠OED=∠OFD;③ED=FD;④EF⊥OC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市举行“第十七届中小学生书法大赛”作品比赛,已知每幅参赛作品成绩记为![]() ,组委会从1000幅书法作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制成如下统计图表.
,组委会从1000幅书法作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制成如下统计图表.
分数段 | 频数 | 百分比 |
| 38 | 0.38 |
|
| 0.32 |
|
|
|
| 10 | 0.1 |
合计 | 100 | 1 |
书法作品比赛成绩频数直方图

根据上述信息,解答下列问题:
(1)请你把表中空白处的数据填写完整.
(2)请补全书法作品比赛成绩频数直方图.
(3)若80分(含80分)以上的书法作品将被评为等级奖,试估计全市获得等级的幅数.
查看答案和解析>>
科目:初中数学 来源: 题型:
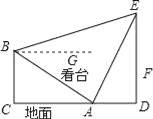
【题目】如图所示,体育场内一看台与地面所成夹角为30°,看台最低点A到最高点B的距离为10![]() ,A,B两点正前方有垂直于地面的旗杆DE.在A,B两点处用仪器测量旗杆顶端E的仰角分别为60°和15°(仰角即视线与水平线的夹角)
,A,B两点正前方有垂直于地面的旗杆DE.在A,B两点处用仪器测量旗杆顶端E的仰角分别为60°和15°(仰角即视线与水平线的夹角)
(1)求AE的长;
(2)已知旗杆上有一面旗在离地1米的F点处,这面旗以0.5米/秒的速度匀速上升,求这面旗到达旗杆顶端需要多少秒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校科技小组进行野外考察,途中遇到一片十几米宽的烂泥湿地.为了安全、迅速地通过这片湿地,他们沿着前进路线铺垫若干块木板,构筑成一条临时通道,从而顺利完成了任务.你能解释他们这样做的道理吗?当人和木板对湿地的压力一定时,随着木板面积S(m2)的变化,人和木板对地面的压强p(Pa)将如何变化?如果人和木板对湿地的压力合计600N,那么:
(1)用含S的代数式表示p,p是S的反比例函数吗?为什么?
(2)当木板面积为0.2m2时,压强是多少?
(3)如果要求压强不超过6000Pa,木板面积至少要多大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com