
【题目】如图①,在平面直角坐标系中,A(a,0),C(b,2),且满足(a+2)2+![]() =0,过C作CB⊥x轴于B.
=0,过C作CB⊥x轴于B.

(1)求三角形ABC的面积;
(2)如图②,若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,求∠AED的度数;
(3)在y轴上是否存在点P,使得三角形ACP和三角形ABC的面积相等?若存在,求出P点的坐标;若不存在,请说明理由.
【答案】(1)4;(2) 45°;(3) P点的坐标为(0,-1)或(0,3).
【解析】试题分析:(1)根据非负数的性质得a+2=0,b-2=0,解得a=-2,b=2,则A(-2,0),C(2,2),B(2,0),然后根据三角形面积公式计算S△ABC;
(2)作EM∥AC,如图②,则AC∥EM∥BD,根据平行线的性质得∠CAE=∠AEM,∠BDE=∠DEM,则∠AED=∠CAE+∠BDE,而∠CAE=![]() ∠CAB,∠BDE=
∠CAB,∠BDE=![]() ∠ODB,所以∠AED=
∠ODB,所以∠AED=![]() (∠CAB+∠ODB),而由AC∥BD得到∠CAB=∠OBD,于是∠CAB+∠ODB=∠OBD+∠ODB=90°,则∠AED=45°;
(∠CAB+∠ODB),而由AC∥BD得到∠CAB=∠OBD,于是∠CAB+∠ODB=∠OBD+∠ODB=90°,则∠AED=45°;
(3)如图③,AC交y轴于Q,先确定Q(0,1),设P(0,t),利用三角形面积公式和S△PAC=S△APQ+S△CPQ=S△ABC得到![]() |t-1|2+
|t-1|2+![]() |t-1|2=4,然后解方程求出t即可得到P点坐标.
|t-1|2=4,然后解方程求出t即可得到P点坐标.
试题解析:(1)∵(a+2)2+![]() =0,
=0,
∴a+2=0,b-2=0,
∴a=-2,b=2,
∴A(-2,0),C(2,2).
∵CB⊥AB,
∴B(2,0),
∴AB=4,CB=2,
则S三角形ABC=![]() ×4×2=4.
×4×2=4.
(2)作EM∥AC,如图②,
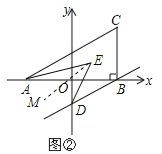
∵AC∥BD,
∴AC∥EM∥BD,
∴∠CAE=∠AEM,∠BDE=∠DEM,
∴∠AED=∠CAE+∠BDE,
∵AE,DE分别平分∠CAB,∠ODB,
∴∠CAE=![]() ∠CAB,∠BDE=
∠CAB,∠BDE=![]() ∠ODB,
∠ODB,
∴∠AED=![]() (∠CAB+∠ODB),
(∠CAB+∠ODB),
∵AC∥BD,
∴∠CAB=∠OBD,
∴∠CAB+∠ODB=∠OBD+∠ODB=90°,
∴∠AED=![]() ×90°=45°.
×90°=45°.
(3)
如图③,AC交y轴于Q,则Q(0,1),
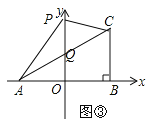
设P(0,t),
∵S△PAC=S△APQ+S△CPQ=S△ABC,
∴![]() |t-1|2+
|t-1|2+![]() |t-1|2=4,解得t=3或t=-1,
|t-1|2=4,解得t=3或t=-1,
∴P点坐标为(0,3),(0,-1);


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:
【题目】佳佳果品店在批发市场购买某种水果销售,第一次用1 200元购进若干千克,并以8元/kg出售,很快售完.由于水果畅销,第二次购买时,每千克的进价比第一次提高了10%,用1 452元所购买的数量比第一次多20 kg,以9元/kg售出100 kg后,因出现高温天气,水果不易保鲜,为减少损失,便降价50%售完剩余的水果.
(1)第一次水果的进价是每千克多少元?
(2)该果品店在这两次销售中,总体上是盈利还是亏损?盈利或亏损了多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,它的三边长是三个连续的正偶数,且AC>BC.
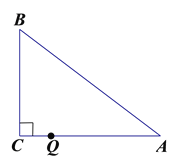
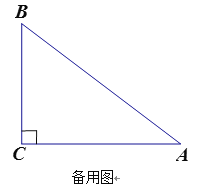
(1)这个直角三角形的各边长;
(2)若动点Q从点C出发,沿CA方向以1个单位长度/秒的速度运动,到达点A停止运动,请运用尺规作图作出以点Q为圆心,QC为半径,且与AB边相切的圆,并求出此时点Q的运动时间.
(3) 若动点Q从点C出发,沿CA方向以1个单位长度/秒的速度运动,到达点A停止运动,以Q为圆心、QC长为半径作圆,请探究点Q在整个运动过程中,运动时间t为怎样的值时,⊙Q与边AB分别有0个公共点、1个公共点和2个公共点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】全民健身和医疗保健是社会普遍关注的问题.2014年,某社区共投入30万元用于购买健身器材和药品.2015年,该社区购买健身器材的费用比上一年增加50%,购买药品的费用比上一年减少![]() ,但社区在这两方面的总投入仍与2014年相同.
,但社区在这两方面的总投入仍与2014年相同.
(1)求2014年社区购买药品的总费用;
(2)据统计,2014年该社区积极健身的家庭达到200户,但其药品费用明显减少,只占当年购买药品总费用的![]() .与2014年相比,如果2015年社区内健身家庭户数增加的百分数与平均每户健身家庭的药品费用降低的百分数相同,那么,2015年该社区用于健身家庭的药品费用就是当年购买健身器材费用的
.与2014年相比,如果2015年社区内健身家庭户数增加的百分数与平均每户健身家庭的药品费用降低的百分数相同,那么,2015年该社区用于健身家庭的药品费用就是当年购买健身器材费用的![]() .求2015年该社区健身家庭的户数.
.求2015年该社区健身家庭的户数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥DE,求证:∠D+∠BCD-∠B=180°.
证明:过点C作CF∥AB.
∵AB∥CF(已知),
∴∠B=________(____________________).
∵AB∥DE,CF∥AB(已知),
∴CF∥DE(__________________________________).
∴∠2+________=180°(________________________).
∵∠2=∠BCD-________(已知),
∴∠D+∠BCD-∠B=180°(等量代换).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解题:
定义:如果一个数的平方等于-1,记为i2=-1,这个数i叫做虚数单位.那么和我们所学的实数对应起来就叫做复数,表示为a+bi(a,b为实数),a叫这个复数的实部,b叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似.
例如计算:(5+i)×(3-4i)=19-17i.
(1)填空:i3= ,i4= .
(2)计算:(3+i)2;
(3)试一试:请利用以前学习的有关知识将![]() 化简成a+bi的形式
化简成a+bi的形式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,并完成填空.
你能比较20152 016和20162 015的大小吗?
为了解决这个问题,先把问题一般化,比较nn+1和(n+1)n(n≥1,且n为整数)的大小.然后从分析n=1,n=2,n=3…的简单情形入手,从中发现规律,经过归纳、猜想得出结论.
(1)通过计算(可用计算器)比较下列①~⑦组两数的大小:(在横线上填上“>”“=”或“<”)
①12____21;②23_____32;③34_____43;④45_____54;
⑤56____65;⑥67_____76;⑦78_____87;
(2)归纳第(1)问的结果,可以猜想出nn+1和(n+1)n的大小关系;
(3)根据以上结论,可以得出20162017和20172016的大小关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形纸片ABCD中,已知AD=8,AB=6,E是边BC上的点,以AE为折痕折叠纸片,使点B落在点F处,连接FC,当△EFC为直角三角形时,BE的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
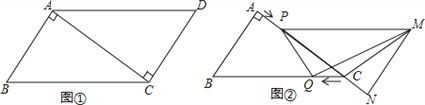
【题目】已知,如图①,在ABCD中,AB=3cm,BC=5cm,AC⊥AB,△ACD沿AC的方向匀速平移得到△PNM,速度为1cm/s;同时,点Q从点C出发,沿CB方向匀速移动,速度为1cm/s,当△PNM停止平移时,点Q也停止移动,如图②,设移动时间为t(s)(0<t<4),连接PQ,MQ,MC,解答下列问题:
(1)当t为何值时,PQ∥MN?
(2)设△QMC的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使S△QMC:S四边形ABQP=1:4?若存在,求出t的值;若不存在,请说明理由.
(4)是否存在某一时刻t,使PQ⊥MQ?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com