
【题目】如图,△ABC中,∠C=90°,它的三边长是三个连续的正偶数,且AC>BC.
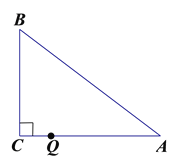
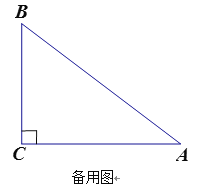
(1)这个直角三角形的各边长;
(2)若动点Q从点C出发,沿CA方向以1个单位长度/秒的速度运动,到达点A停止运动,请运用尺规作图作出以点Q为圆心,QC为半径,且与AB边相切的圆,并求出此时点Q的运动时间.
(3) 若动点Q从点C出发,沿CA方向以1个单位长度/秒的速度运动,到达点A停止运动,以Q为圆心、QC长为半径作圆,请探究点Q在整个运动过程中,运动时间t为怎样的值时,⊙Q与边AB分别有0个公共点、1个公共点和2个公共点?
【答案】(1)6,8,10;(2)t=3;(3)当0<t<3时,⊙Q与边AB有0个公共点,
当t=3或4<t≤8时,⊙Q与边AB有1个公共点,
当3<t≤4时,⊙Q与边AB有2个公共点.
【解析】【试题分析】(1)根据直角△ABC的三边长是三个连续的正偶数,设最短的边为x,则另两边分别为x+2,x+4.根据勾股定理得:(x+4)2=x2+(x+2)2,解得x1=6,x2=-2(舍去),三边长分别是6,8,10.
(2)设⊙Q与AB相切与点P.根据切线的性质得:∠BPQ=90°,由于∠C=90°,根据切线的判定得,BC与⊙Q 相切,根据切线长定理得,BC=BP=6,AP=4
设CQ=x,则AQ=8-x在Rt![]() 中,利用勾股定理得:AQ2=PQ2+AP2,即(8-x)2=x2+42
中,利用勾股定理得:AQ2=PQ2+AP2,即(8-x)2=x2+42
解得:x=3,即t=3
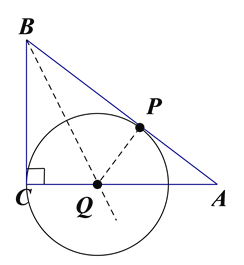
(3)根据(2)的求解,依据数形结合思想,易得:当0<t<3时,⊙Q与边AB有0个公共点;当t=3或4<t≤8时,⊙Q与边AB有1个公共点;当3<t≤4时,⊙Q与边AB有2个公共点.
【试题解析】
(1)设最短的边为x,则另两边分别为x+2,x+4.
根据题意,得:(x+4)2=x2+(x+2)2
整理得x2-4x-12=0,解得x1=6,x2=-2(舍去)
三边长分别是6,8,10.
(2)设⊙Q与AB相切与点P
∴∠BPQ=90°
∵∠C=90°
∴BC与⊙Q 相切
∴BC=BP=6
∴AP=4
设CQ=x,则AQ=8-x
∵AQ2=PQ2+AP2
∴(8-x)2=x2+42
∴x=3
即t=3
(3)当0<t<3时,⊙Q与边AB有0个公共点,
当t=3或4<t≤8时,⊙Q与边AB有1个公共点,
当3<t≤4时,⊙Q与边AB有2个公共点.



科目:初中数学 来源: 题型:
【题目】根据下列证明过程填空:
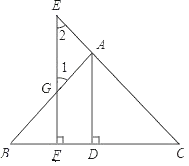
已知:如 图,AD⊥BC于点D,EF⊥BC于点F,交AB于点G,交CA的延长线于点E,∠1=∠2.
求证:AD平分∠BAC,填写证明中的空白.
证明:
∵AD⊥BC,EF⊥BC (已知),
∴EF∥AD ( ),
∴ = ( 两直线平行,内错角相等 ),
=∠CAD ( ).
∵ (已知),
∴ ,即AD平分∠BAC ( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应我市“中国梦”“宜宾梦”主题教育活动,某中学在全校学生中开展了以“中国梦我的梦”为主题的征文比赛,评选出一、二、三等奖和优秀奖.小明同学根据获奖结果,绘制成如图所示的统计表和数学统计图.
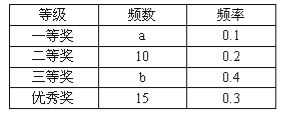
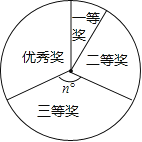
请你根据以上图表提供的信息,解答下列问题:
(1)a= ,b= ,n= .
(2)学校决定在获得一等奖的作者中,随机推荐两名作者代表学校参加市级比赛,其中王梦、李刚都获得一等奖,请用画树状图或列表的方法,求恰好选中这二人的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列一元二次方程中,两实根之和为1的是 ( )
A. x2—x+1=0 B. x2+x—3=0 C. 2 x2-x-1=0 D. x2-x-5=0
查看答案和解析>>
科目:初中数学 来源: 题型:
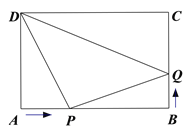
【题目】如图,在矩形ABCD中,AB=10cm,AD=8cm,点P从点A出发沿AB以2cm/s的速度向点终点B运动,同时点Q从点B出发沿BC以1cm/s的速度向点终点C运动,它们到达终点后停止运动.
(1)几秒后,点P、D的距离是点P、Q的距离的2倍;
(2)几秒后,△DPQ的面积是24cm2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一张三角形纸片ABC(如图甲),其中AB=AC.将纸片沿过点B的直线折叠,使点C落到AB边上的E点处,折痕为BD(如图乙).再将纸片沿过点E的直线折叠,点A恰好与点D重合,折痕为EF(如图丙).原三角形纸片ABC中,∠ABC的大小为______°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2015桂林)“全民阅读”深入人心,好读书,读好书,让人终身受益.为满足同学们的读书需求,学校图书馆准备到新华书店采购文学名著和动漫书两类图书.经了解,20本文学名著和40本动漫书共需1520元,20本文学名著比20本动漫书多440元(注:所采购的文学名著价格都一样,所采购的动漫书价格都一样).
(1)求每本文学名著和动漫书各多少元?
(2)若学校要求购买动漫书比文学名著多20本,动漫书和文学名著总数不低于72本,总费用不超过2000元,请求出所有符合条件的购书方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系中,A(a,0),C(b,2),且满足(a+2)2+![]() =0,过C作CB⊥x轴于B.
=0,过C作CB⊥x轴于B.

(1)求三角形ABC的面积;
(2)如图②,若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,求∠AED的度数;
(3)在y轴上是否存在点P,使得三角形ACP和三角形ABC的面积相等?若存在,求出P点的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com