
【题目】近年来,青少年中的近视眼和肥胖案例日趋增多,人们普遍意识到健康的身体是学习的保障,所以体育活动越来越受重视.某商店分两次购进跳绳和足球两种商品进行销售,每次购进同一种商品的进价相同,具体情况如下表所示.
购进数量(件) | 购进所需费用(元) | ||
跳绳 | 足球 | ||
第一次 | 30 | 40 | 3800 |
第二次 | 40 | 30 | 3200 |
(1)跳绳和足球两种商品每件的进价分别是多少元?
(2)商店计划用5300元的资金进行第三次进货,共购进跳绳和足球两种商品100件,其中要求足球的数量不少于跳绳的数量,有哪几种进货方案?
【答案】(1)每根跳绳的进价为20元,每个足球的进价为80元;(2)共有以下6种进货方案,具体方案见解析.
【解析】
(1)设跳绳的进价为x元,足球的进价为y元,根据前两次进货的数量及总价,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)设购进跳绳m根,则购进足球(100-m)个,由B商品的数量不少于A商品的数量且总价不超过5300元,即可得出关于m的一元一次不等式组,解之即可得出m的取值范围,结合m为整数即可得出各进货方案.
(1)设每根跳绳的进价为![]() 元,每个足球的进价为
元,每个足球的进价为![]() 元.
元.
依题意,得![]() 解得
解得![]()
答:每根跳绳的进价为20元,每个足球的进价为80元.
(2)设购进跳绳![]() 根,则购进足球
根,则购进足球![]() 个.
个.
由![]() ,得
,得![]() ,由
,由![]() ,得
,得![]() ,则有
,则有![]() .
.
∵![]() 为整数,∴
为整数,∴![]() 的值可能为45,46,47,48,49,50,
的值可能为45,46,47,48,49,50,
∴共有以下6种进货方案:
方案一:购进跳绳45根,则购进足球55个.
方案二:购进跳绳46根,则购进足球54个.
方案三:购进跳绳47根,则购进足球53个.
方案四:购进跳绳48根,则购进足球52个.
方案五:购进跳绳49根,则购进足球51个.
方案六:购进跳绳50根,则购进足球50个.


科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.

(1)求证:CE=CF;
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
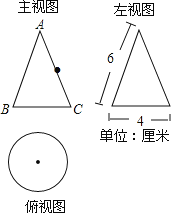
【题目】如图是一个几何体的三视图.
(1)写出该几何体的名称,并根据所示数据计算这个几何体的表面积;
(2)如果一只蚂蚁要从这个几何体中的点B出发,沿表面爬到AC的中点D,请你求出这个线路的最短路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
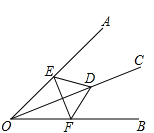
【题目】如图,已知射线OC上的任意一点到∠AOB的两边的距离都相等,点D、E、F分别为边OC、OA、OB上,如果要想证得OE=OF,只需要添加以下四个条件中的某一个即可,请写出所有可能的条件的序号__________.
①∠ODE=∠ODF;②∠OED=∠OFD;③ED=FD;④EF⊥OC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市举行“第十七届中小学生书法大赛”作品比赛,已知每幅参赛作品成绩记为![]() ,组委会从1000幅书法作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制成如下统计图表.
,组委会从1000幅书法作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制成如下统计图表.
分数段 | 频数 | 百分比 |
| 38 | 0.38 |
|
| 0.32 |
|
|
|
| 10 | 0.1 |
合计 | 100 | 1 |
书法作品比赛成绩频数直方图

根据上述信息,解答下列问题:
(1)请你把表中空白处的数据填写完整.
(2)请补全书法作品比赛成绩频数直方图.
(3)若80分(含80分)以上的书法作品将被评为等级奖,试估计全市获得等级的幅数.
查看答案和解析>>
科目:初中数学 来源: 题型:
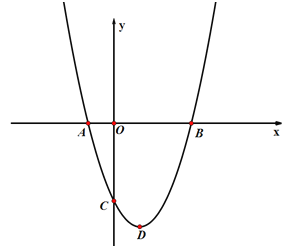
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于A、B两点(点A在点B的左侧),点B的坐标为(3,0),与
轴交于A、B两点(点A在点B的左侧),点B的坐标为(3,0),与![]() 轴交于点C(0,-3),顶点为D.
轴交于点C(0,-3),顶点为D.
(1)求抛物线的解析式及顶点D的坐标.
(2)联结AC,BC,求∠ACB的正切值.
(3)点P是x轴上一点,是否存在点P使得△PBD与△CAB相似,若存在,请求出点P的坐标;若不存在,请说明理由.
(4)M是抛物线上一点,点N在![]() 轴,是否存在点N,使得以点A,C,M,N为顶点的四边形是平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
轴,是否存在点N,使得以点A,C,M,N为顶点的四边形是平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
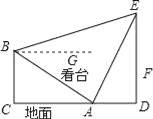
【题目】如图所示,体育场内一看台与地面所成夹角为30°,看台最低点A到最高点B的距离为10![]() ,A,B两点正前方有垂直于地面的旗杆DE.在A,B两点处用仪器测量旗杆顶端E的仰角分别为60°和15°(仰角即视线与水平线的夹角)
,A,B两点正前方有垂直于地面的旗杆DE.在A,B两点处用仪器测量旗杆顶端E的仰角分别为60°和15°(仰角即视线与水平线的夹角)
(1)求AE的长;
(2)已知旗杆上有一面旗在离地1米的F点处,这面旗以0.5米/秒的速度匀速上升,求这面旗到达旗杆顶端需要多少秒?
查看答案和解析>>
科目:初中数学 来源: 题型:
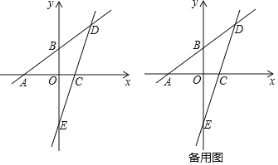
【题目】已知:如图,一次函数y=![]() x+3的图象分别与x轴、y轴相交于点A、B,且与经过点C(2,0)的一次函数y=kx+b的图象相交于点D,点D的横坐标为4,直线CD与y轴相交于点E.
x+3的图象分别与x轴、y轴相交于点A、B,且与经过点C(2,0)的一次函数y=kx+b的图象相交于点D,点D的横坐标为4,直线CD与y轴相交于点E.
(1)直线CD的函数表达式为______;(直接写出结果)
(2)在x轴上求一点P使△PAD为等腰三角形,直接写出所有满足条件的点P的坐标.
(3)若点Q为线段DE上的一个动点,连接BQ.点Q是否存在某个位置,将△BQD沿着直线BQ翻折,使得点D恰好落在直线AB下方的y轴上?若存在,求点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com