练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】某市为了节约用水，对自来水的收费标准作如下规定：每月每户用水不超过10吨的部分，按2元/吨收费；超过10吨的部分按2．5元/吨收费．

    （1）若黄老师家5月份用水16吨，问应交水费多少元？

    （2）若黄老师家7月用水a吨，问应交水费多少元？（用a的代数式表示）

    【答案】（1）35；（2） 当0＜a≤10时，应交水费为2a元；②当a＞10时，应交水费为元．

    【解析】试题（1）按照自来水的收费标准，黄老师应交水费：10×2+（所用水的重量-10）×2．5；（2）黄老师家7月用水a吨，根据a的大小及自来水的收费标准可得黄老师应缴纳的水费分①当0＜a≤10时和当a＞10时两种情况，根据这两种情况分别表示出黄老师应缴纳的水费即可．

    试题解析：解：（1）（元）答：应交水费35元．

    （2）①当0＜a≤10时，应交水费为2a（元）．

    ②当a＞10时，应交水费为：（元）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】下列四个选项中，不是y关于x的函数的是（ ）

    A．|y|=x﹣1 B．y= C．y=2x﹣7 D．y=x2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

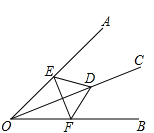
    【题目】如图，已知射线OC上的任意一点到∠AOB的两边的距离都相等，点D、E、F分别为边OC、OA、OB上，如果要想证得OE=OF，只需要添加以下四个条件中的某一个即可，请写出所有可能的条件的序号__________．

    ①∠ODE=∠ODF；②∠OED=∠OFD；③ED=FD；④EF⊥OC．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

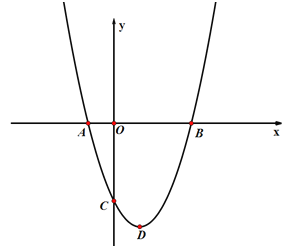
    【题目】如图，在平面直角坐标系中，抛物线与轴交于A、B两点（点A在点B的左侧），点B的坐标为（3，0），与轴交于点C（0，-3），顶点为D．

    （1）求抛物线的解析式及顶点D的坐标．

    （2）联结AC，BC，求∠ACB的正切值．

    （3）点P是x轴上一点，是否存在点P使得△PBD与△CAB相似，若存在，请求出点P的坐标；若不存在，请说明理由．

    （4）M是抛物线上一点，点N在轴，是否存在点N，使得以点A，C，M，N为顶点的四边形是平行四边形？若存在，请直接写出点N的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

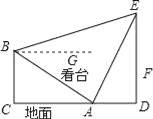
    【题目】如图所示，体育场内一看台与地面所成夹角为30°，看台最低点A到最高点B的距离为10，A，B两点正前方有垂直于地面的旗杆DE．在A，B两点处用仪器测量旗杆顶端E的仰角分别为60°和15°（仰角即视线与水平线的夹角）

    （1）求AE的长；

    （2）已知旗杆上有一面旗在离地1米的F点处，这面旗以0.5米/秒的速度匀速上升，求这面旗到达旗杆顶端需要多少秒？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，排球运动员站在点处练习发球，将球从点正上方的处发出，把球看成点，其运行的高度与运行的水平距离满足关系式．已知球网与点的水平距离为，高度为，球场的边界距点的水平距离为．

    （）求与的关系式（不要求写出自变量的取值范围）．

    （）球能否越过球网？球会不会出界？请说明理由．

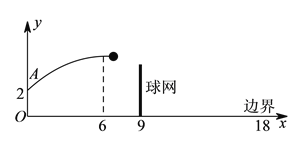
    查看答案和解析>>

    科目：初中数学 来源： 题型：

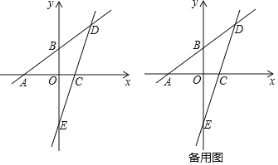
    【题目】已知：如图，一次函数y=x+3的图象分别与x轴、y轴相交于点A、B，且与经过点C(2，0)的一次函数y=kx+b的图象相交于点D，点D的横坐标为4，直线CD与y轴相交于点E．

    (1)直线CD的函数表达式为______；(直接写出结果)

    (2)在x轴上求一点P使△PAD为等腰三角形，直接写出所有满足条件的点P的坐标．

    (3)若点Q为线段DE上的一个动点，连接BQ．点Q是否存在某个位置，将△BQD沿着直线BQ翻折，使得点D恰好落在直线AB下方的y轴上？若存在，求点Q的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】四边形ABCD是边长为4的正方形，点P是平面内一点．且满足BP⊥PC，现将点P绕点D顺时针旋转90度，则CQ的最大值=_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下面材料：

    小伟遇到这样一个问题：如图1，在△ABC（其中∠BAC是一个可以变化的角）中，AB=2，AC=4，以BC为边在BC的下方作等边△PBC，求AP的最大值．

    小伟是这样思考的：利用变换和等边三角形将边的位置重新组合．他的方法是以点B为旋转中心将△ABP逆时针旋转60°得到△A′BC，连接A′A，当点A落在A′C上时，此题可解（如图2）．

    请你回答：AP的最大值是　 　．

    参考小伟同学思考问题的方法，解决下列问题：

    如图3，等腰Rt△ABC．边AB=4，P为△ABC内部一点，则AP+BP+CP的最小值是　 　．（结果可以不化简）

    查看答案和解析>>

    同步练习册答案