
【题目】如图,已知∠DAB+∠D=180°,AC平分∠DAB,且∠CAD=25°,∠B=95°
(1)求∠DCA的度数;
(2)求∠DCE的度数.
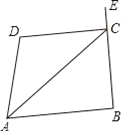
【答案】(1)25°.(2)95°.
【解析】试题分析:(1)利用角平分线的定义可以求得∠DAB的度数,再依据∠DAB+∠D=180°求得∠D的度数,在△ACD中利用三角形的内角和定理.即可求得∠DCA的度数;
(2)根据(1)可以证得:AB∥DC,利用平行线的性质定理即可求解.
解:(1)∵AC平分∠DAB,
∴∠CAB=∠DAC=25°,
∴∠DAB=50°,
∵∠DAB+∠D=180°,
∴∠D=180°﹣50°=130°,
∵△ACD中,∠D+∠DAC+∠DCA=180°,
∴∠DCA=180°﹣130°﹣25°=25°.
(2)∵∠DAC=25°,∠DCA=25°,
∴∠DAC=∠DCA,
∴AB∥DC,
∴∠DCE=∠B=95°.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在今年“全国助残日”捐款活动中,某班级第一小组7名同学积极捐出自己的零花钱,奉献自己的爱心.他们捐款的数额分别是(单位:元)50,20,50,30,25,50,55,这组数据的众数和中位数分别是( ).
A. 50元,30元B. 50元,40元
C. 50元,50元D. 55元,50元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:已知点P(x0,y0)和直线y=kx+b,则点P到直线y=kx+b的距离,可用公式d=![]() 计算.
计算.
例如:求点P(﹣1,2)到直线y=3x+7的距离.
解:因为直线y=3x+7,其中k=3,b=7.
所以点P(﹣1,2)到直线y=3x+7的距离为:d=![]() =
=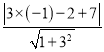 =
=![]() =
=![]() .
.
根据以上材料,解答下列问题:
(1)求点P(1,﹣1)到直线y=x﹣1的距离;
(2)已知⊙Q的圆心Q坐标为(0,5),半径r为2,判断⊙Q与直线y=![]() x+9的位置关系并说明理由;
x+9的位置关系并说明理由;
(3)已知直线y=﹣2x+4与y=﹣2x﹣6平行,求这两条直线之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在 2008 年的一次抗震救灾大型募捐活动中,文艺工作者积极向灾区捐款.其中 10 人 的捐款分别是:5 万,8 万,10 万,10 万,10 万,20 万,20 万,30 万,50 万,100 万.这组数据的众数和中位数分别是( )
A. 10 万,15 万B. 10 万,20 万C. 20 万,15 万D. 20 万,10 万
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4)

(1)请画出△ABC向左平移6个单位长度后得到的△A1B1C1;
(2)以点O为位似中心,将△ABC缩小为原来的![]() ,得到△A2B2C2,请在y轴右侧画出△A2B2C2,并求出∠A2C2B2的正弦值.
,得到△A2B2C2,请在y轴右侧画出△A2B2C2,并求出∠A2C2B2的正弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两人各抛一枚硬币,则下面说法正确的是( )
A. 每次抛出后出现正面或反面是一样的
B. 抛掷同样的次数,则出现正、反面的频数一样多
C. 在相同条件下,即使抛掷的次数很多,出现正、反面的频数也不一定相同
D. 当抛掷次数很多时,出现正、反面的次数就相同了
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com