
【题目】某兴趣小组开展课外活动.如图,A,B两地相距12米,小明从点A出发沿AB方向匀速前进,2秒后到达点D,此时他(CD)在某一灯光下的影长为AD,继续按原速行走2秒到达点F,此时他在同一灯光下的影子仍落在其身后,并测得这个影长为1.2米,然后他将速度提高到原来的1.5倍,再行走2秒到达点H,此时他(GH)在同一灯光下的影长为BH(点C,E,G在一条直线上).
(1)请在图中画出光源O点的位置,并画出他位于点F时在这个灯光下的影长FM(不写画法)
(2)求小明原来的速度。
【答案】
(1)
解:如图,
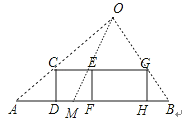
(2)
解:设小明原来的速度为xm/s,则CE=2xm,AM=AF﹣MF=(4x﹣1.2)m,EG=2×1.5x=3xm,BM=AB﹣AM=12﹣(4x﹣1.2)=13.2﹣4x,
∵点C,E,G在一条直线上,CG∥AB,
∴△OCE∽△OAM,△OEG∽△OMB,
∴![]() =
=![]() ,
,![]() =
=![]() ,
,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得x=1.5,经检验x=1.5为方程的解,
∴小明原来的速度为1.5m/s.
答:小明原来的速度为1.5m/s.
【解析】(1)利用中心投影的定义画图;
(2)设小明原来的速度为xm/s,则CE=2xm,AM=AF﹣MF=(4x﹣1.2)m,EG=2×1.5x=3xm,BM=AB﹣AM=12﹣(4x﹣1.2)=13.2﹣4x,根据相似三角形的判定方法得到△OCE∽△OAM,△OEG∽△OMB,列出方程求解即可
【考点精析】解答此题的关键在于理解相似三角形的应用的相关知识,掌握测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解,以及对中心投影的理解,了解手电筒、路灯和台灯的光线可以看成是从一个点发出的,这样的光线所形成的投影称为中心投影;作一物体中心投影的方法:过投影中心与物体顶端作直线,直线与投影面的交点与物体的底端之间的线段即为物体的影子.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,点E,F分别是边BC,AB上的点,且CE=BF,连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC. 
(1)请判断:FG与CE的数量关系是 , 位置关系是;
(2)如图2,若点E、F分别是CB、BA延长线上的点,其它条件不变,(1)中结论是否仍然成立?请出判断判断并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种商品的进价为40元/件,以获利不低于25%的价格销售时,商品的销售单价y(元/件)与销售数量x(件)(x是正整数)之间的关系如下表:
x(件) | … | 5 | 10 | 15 | 20 | … |
y(元/件) | … | 75 | 70 | 65 | 60 | … |
(1)由题意知商品的最低销售单价是___元,当销售单价不低于最低销售单价时,y是x的一次函数.求出y与x的函数关系式及x的取值范围;
(2)在(1)的条件下,当销售单价为多少元时,所获销售利润最大,最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线AC,BD相交于点O,分别延长OA,OC到点E,F,使AE=CF,依次连接B,F,D,E各点.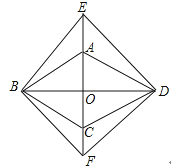
(1)求证:△BAE≌△BCF
(2)若∠ABC=50°,则当∠EBA=°时,四边形BFDE是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线l⊥AB于点B,点C在AB上,且AC:CB=2:1,点M是直线l上的动点,作点B关于直线CM的对称点B′,直线AB′与直线CM相交于点P,连接PB.
(1)如图2,若点P与点M重合,则∠PAB= , 线段PA与PB的比值为 
(2)如图3,若点P与点M不重合,设过P,B,C三点的圆与直线AP相交于D,连接CD,求证:①CD=CB′;②PA=2PB
(3)如图4,若AC=2,BC=1,则满足条件PA=2PB的点都在一个确定的圆上,在以下小题中选做一题:
①如果你能发现这个确定的圆的圆心和半径,那么不必写出发现过程,只要证明这个圆上的任意一点Q,都满足QA=2QB;
②如果你不能发现这个确定的圆的圆心和半径,那么请取出几个特殊位置的P点,如点P在直线AB上,点P与点M重合等进行探究,求这个圆的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.
(1)求证:四边形BFCE是平行四边形
(2)若AD=10,DC=3,∠EBD=60°,则BE= 时,四边形BFCE是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△OAB的顶点A(﹣4,8)在抛物线y=ax2上,将Rt△OAB绕点O顺时针旋转90°,得到△OCD,边CD与该抛物线交于点P,则点P的坐标为 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com