
【题目】如图1,直线l⊥AB于点B,点C在AB上,且AC:CB=2:1,点M是直线l上的动点,作点B关于直线CM的对称点B′,直线AB′与直线CM相交于点P,连接PB.
(1)如图2,若点P与点M重合,则∠PAB= , 线段PA与PB的比值为 
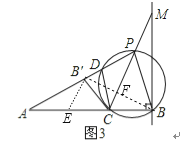
(2)如图3,若点P与点M不重合,设过P,B,C三点的圆与直线AP相交于D,连接CD,求证:①CD=CB′;②PA=2PB
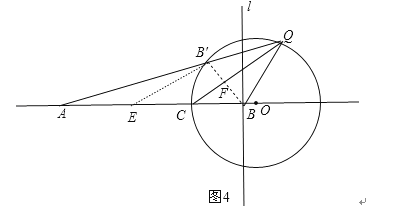
(3)如图4,若AC=2,BC=1,则满足条件PA=2PB的点都在一个确定的圆上,在以下小题中选做一题:
①如果你能发现这个确定的圆的圆心和半径,那么不必写出发现过程,只要证明这个圆上的任意一点Q,都满足QA=2QB;
②如果你不能发现这个确定的圆的圆心和半径,那么请取出几个特殊位置的P点,如点P在直线AB上,点P与点M重合等进行探究,求这个圆的半径.
【答案】
(1)30°;2
(2)
证明:①∵B关于直线CM的对称点为点B′,
∴△PBC沿PC翻折得到△PB′C,
∴∠PB′C=∠PBC,
∵∠CDB′=∠CBP,
∴∠CDB′=∠CB′D,
∴CD=CB′;
②作B′E∥PC交AC于E,连结BB′交PC于F,如图3,
∵B关于直线CM的对称点为点B′,
∴FB=FB′,PB=PB′,
而CF∥B′E,
∴BC=CE,
∵AC=2BC,
∴AE=EC,
而B′E∥PC,
∴AB′=PB′,
∴PA=2PB′=2PB
(3)
解:选①.
证明:作B′E∥QC交AC于E,连结BB′交QC于F,如图4,
∵B关于直线CM的对称点为点B′,
∴FB=FB′,QB=QB′,
而CF∥B′E,
∴BC=CE,
∵AC=2BC,
∴AE=EC,
而B′E∥QC,
∴AB′=QB′,
∴PA=2QB′=2QB.
【解析】(1)如图2,根据对称性质得△PBC沿PC翻折得到△PB′C,根据折叠性质得CB′=CB,∠PB′C=∠PBC=90°,由于AC:CB=2:1,则AC=2CB′,然后在Rt△AB′C中,利用正弦定义可计算出∠A=30°,再利用含30度的直角三角形三边的关系易得PA=2PB;
(2)①与(1)一样可得∠PB′C=∠PBC,再根据圆内接四边形的性质得∠CDB′=∠CBP,所以∠CDB′=∠CB′D,于是根据等腰三角形的判定得到CD=CB′;
②作B′E∥PC交AC于E,连结BB′交PC于F,如图3,利用对称性质得FB=FB′,PB=PB′,而CF∥B′E,则CF为△BEB′的中位线,所以BC=CE,加上AC=2BC,所以AE=EC,然后利用B′E∥PC,则AB′=PB′,所以PA=2PB′=2PB;
(3)选①进行证明,作B′E∥QC交AC于E,连结BB′交QC于F,如图4,与(2)中②的证明方法一样.


科目:初中数学 来源: 题型:
【题目】如图,已知直线y=ax+b与双曲线y=![]() (x>0)交于A(x1 , y1),B(x2 , y2)两点(A与B不重合),直线AB与x轴交于P(x0 , 0),与y轴交于点C.
(x>0)交于A(x1 , y1),B(x2 , y2)两点(A与B不重合),直线AB与x轴交于P(x0 , 0),与y轴交于点C.
(1)若A,B两点坐标分别为(1,3),(3,y2),求点P的坐标.
(2)若b=y1+1,点P的坐标为(6,0),且AB=BP,求A,B两点的坐标.
(3)结合(1),(2)中的结果,猜想并用等式表示x1 , x2 , x0之间的关系(不要求证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某兴趣小组开展课外活动.如图,A,B两地相距12米,小明从点A出发沿AB方向匀速前进,2秒后到达点D,此时他(CD)在某一灯光下的影长为AD,继续按原速行走2秒到达点F,此时他在同一灯光下的影子仍落在其身后,并测得这个影长为1.2米,然后他将速度提高到原来的1.5倍,再行走2秒到达点H,此时他(GH)在同一灯光下的影长为BH(点C,E,G在一条直线上).
(1)请在图中画出光源O点的位置,并画出他位于点F时在这个灯光下的影长FM(不写画法)
(2)求小明原来的速度。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“2015扬州鉴真国际半程马拉松”的赛事共有三项:A.“半程马拉松”、B.“10公里”、C.“迷你马拉松”.小明和小刚参与了该项赛事的志愿者服务工作,组委会随机将志愿者分配到三个项目组.
(1)小明被分配到“迷你马拉松”项目组的概率为 。
(2)求小明和小刚被分配到不同项目组的概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两个不透明的布袋,甲袋中有两个完全相同的小球,分别标有数字1和﹣2;乙袋中有三个完全相同的小球,分别标有数字﹣1、0和2.小丽先从甲袋中随机取出一个小球,记录下小球上的数字为x;再从乙袋中随机取出一个小球,记录下小球上的数字为y,设点P的坐标为(x,y).
(1)请用表格或树状图列出点P所有可能的坐标。
(2)求点P在一次函数y=x+1图象上的概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,以对角线AC为边作第二个正方形,再以对角线AE为边作第三个正方形AEGH,如此下去,第n个正方形的边长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,观测点A、旗杆DE的底端D、某楼房CB的底端C三点在一条直线上,从点A处测得楼顶端B的仰角为22°,此时点E恰好在AB上,从点D处测得楼顶端B的仰角为38.5°.已知旗杆DE的高度为12米,试求楼房CB的高度.(参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,sin38.5°≈0.62,cos38.5°≈0.78,tan38.5°≈0.80)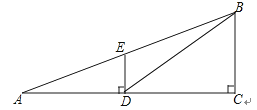
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD内接于⊙O,如图所示,在劣弧 ![]() 上取一点E,连接DE、BE,过点D作DF∥BE交⊙O于点F,连接BF、AF,且AF与DE相交于点G,求证:
上取一点E,连接DE、BE,过点D作DF∥BE交⊙O于点F,连接BF、AF,且AF与DE相交于点G,求证: 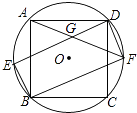
(1)四边形EBFD是矩形;
(2)DG=BE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com