
【题目】已知射线![]() 与直线
与直线![]() 交于点
交于点![]() ,
,![]() 平分
平分![]() ,
,![]() 于点
于点![]() ,
,![]() .
.
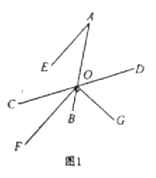
(1)如图1,若![]() ;
;
①求![]() 的度数;
的度数;
②试说明![]() 平分
平分![]() .
.
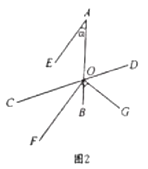
(2)如图2,设![]() 的度数为
的度数为![]() ,当为多少度时,射线
,当为多少度时,射线![]() 是
是![]() 的三等分线?并说明理由.
的三等分线?并说明理由.
【答案】(1)①150°;②说明见解析;(2)18°或45°,说明见解析.
【解析】
(1)①根据题意可求∠BOF=30°,由平角定义可求∠DOF的度数
②通过题意可求∠AOD=∠BOG=60°,即可得OD平分∠AOG
(2)设∠AOD=β,分∠AOD=2∠DOG,或∠DOG=2∠AOD,两种情况讨论,根据题意可列方程,可求β的值,即可得α的值.
(1)①∵AE∥OF
∴∠A=∠BOF
∵OF平分∠COF
∴∠BOC=60°,∠COF=30°
∴∠DOF=180-30°=150°
②∵∠BOC=60°
∴∠AOD=60°
∵OF⊥OG
∴∠BOF+∠FOG=90°
∴∠BOG=60°
∵∠BOG+∠DOG+∠AOD=180°
∴∠DOG=60°=∠AOD
∴OD平分∠AOG
(2)设∠AOD=β
∵射线OD是∠AOG的三等分线
∴∠AOD=2∠DOG,或∠DOG=2∠AOD
若∠AOD=2∠DOG
∴∠DOG=![]() β
β
∵∠BOC=∠AOD,OF平分∠BOC
∴∠BOF=![]() β
β
∵OF⊥OG
∴∠BOG=90-![]() α
α
∵∠BOG+∠DOG+∠AOD=180°
∴![]() β+90-
β+90-![]() β+β=180°
β+β=180°
∴∠β=90°
∴∠BOF=45°
∵OF∥AE
∴∠A=∠BOF=45°
即α=45°
若∠DOG=2∠AOD=2β
∵∠BOC=∠AOD,OF平分∠BOC
∴∠BOF=![]() β
β
∵OF⊥OG
∴∠BOG=90-![]() α
α
∵∠BOG+∠DOG+∠AOD=180°
∴2β+90-![]() β+β=180°
β+β=180°
∴∠β=36°
∴∠BOF=18°
∴OF∥AE
∴∠A=∠BOF=18°
∴α=18°
综上所述α为18°或45°


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】我国南宋著名数学家秦九韶的著作《数书九章》里记载着这样一道题:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题的大意是:有一块三角形沙田,三条边长分别为5里;12里;13里,问这块沙田面积有多大?题中的1里=0.5千米,则该沙田的面积为( )
A.3平方千米B.7.5平方千米C.15平方千米D.30平方千米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O.已知∠BOD=75°,OE把∠AOC分成两个角,且∠AOE:∠EOC=2:3.
(1)求∠AOE的度数;
(2)若OF平分∠BOE,问:OB是∠DOF的平分线吗?试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题情境】
如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.

【探究展示】
(1)证明:AM=AD+MC;
(2)AM=DE+BM是否成立?若成立,请给出证明;若不成立,请说明理由.
【拓展延伸】
(3)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,探究展示(1)、(2)中的结论是否成立?请分别作出判断,不需要证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了更好的治理西流湖水质,保护环境,市治污公司决定购买 10 台污水处理设备.现有 A、B 两种型号的设备,其中每台的价格,月处理污水量如下表:
A 型 | B 型 | |
价格(万元/台) | a | b |
处理污水量(吨/月) | 240 | 200 |
经调查:购买一台 A 型设备比购买一台 B 型设备多 2 万元,购买 2 台 A 型设备比购买 3 台 B 型设备少 6 万元.
(1)求 a,b 的值;
(2)经预算:市治污公司购买污水处理设备的资金不超过 105 万元,你认为该公司 有哪几种购买方案;
(3)在(2)问的条件下,若每月要求处理西流湖的污水量不低于 2040 吨,为了节 约资金,请你为治污公司设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直角三角形![]() 中,
中,![]() ,直线
,直线![]() 过点
过点![]() .
.
(1)当![]() 时,如图①,分别过点
时,如图①,分别过点![]() 、
、![]() 作
作![]() 于点
于点![]() ,
,![]() 于点
于点![]() .求证:
.求证:![]() .
.
(2)当![]() ,
,![]() 时,如图②,点
时,如图②,点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,连接
对称,连接![]() 、
、![]() ,动点
,动点![]() 从点
从点![]() 出发,以每秒1个单位长度的速度沿
出发,以每秒1个单位长度的速度沿![]() 边向终点
边向终点![]() 运动,同时动点
运动,同时动点![]() 从点
从点![]() 出发,以每秒3个单位的速度沿
出发,以每秒3个单位的速度沿![]() 向终点
向终点![]() 运动,点
运动,点![]() 、
、![]() 到达相应的终点时停止运动,过点
到达相应的终点时停止运动,过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,设运动时间为
,设运动时间为![]() 秒.
秒.
①用含![]() 的代数式表示
的代数式表示![]() .
.
②直接写出当![]() 与
与![]() 全等时
全等时![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一元二次方程mx2-2mx+m-2=0.
(1)若方程有两个不等实数根,求m的取值范围;
(2)若方程的两实数根为x1,x2,且|x1-x2|=1,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个转盘被平均分成12份,每份上写上不同的数字,游戏方法:先猜数后转动转盘,若指针指向的数字与所猜的数一致,则猜数者获胜.现提供三种猜数方法:
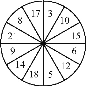
①猜是“奇数”,或是“偶数”;
②猜是“大于10的数”,或是“不大于10的数”;
③猜是“3的倍数”,或是“不是3的倍数”.
如果你是猜数者,你愿意选择哪一种猜数方法?怎样猜?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com