
【题目】直角三角形![]() 中,
中,![]() ,直线
,直线![]() 过点
过点![]() .
.
(1)当![]() 时,如图①,分别过点
时,如图①,分别过点![]() 、
、![]() 作
作![]() 于点
于点![]() ,
,![]() 于点
于点![]() .求证:
.求证:![]() .
.
(2)当![]() ,
,![]() 时,如图②,点
时,如图②,点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,连接
对称,连接![]() 、
、![]() ,动点
,动点![]() 从点
从点![]() 出发,以每秒1个单位长度的速度沿
出发,以每秒1个单位长度的速度沿![]() 边向终点
边向终点![]() 运动,同时动点
运动,同时动点![]() 从点
从点![]() 出发,以每秒3个单位的速度沿
出发,以每秒3个单位的速度沿![]() 向终点
向终点![]() 运动,点
运动,点![]() 、
、![]() 到达相应的终点时停止运动,过点
到达相应的终点时停止运动,过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,设运动时间为
,设运动时间为![]() 秒.
秒.
①用含![]() 的代数式表示
的代数式表示![]() .
.
②直接写出当![]() 与
与![]() 全等时
全等时![]() 的值.
的值.

【答案】(1)证明见解析;(2)①CN=6-3t;(2)3.5秒或5秒或6.5秒
【解析】
(1)根据垂直的定义得到∠DAC=∠ECB,利用AAS定理证明△ACD≌△CBE;
(2)①由题意得,AM=t,FN=3t,则CM=8-t,由折叠的性质可知,CF=CB=6,即可得出结果;
②分点F沿F→C路径运动,点F沿C→B路径运动,点F沿B→C路径运动,点F沿C→F路径运动四种情况,根据全等三角形的判定定理列式计算.
(1)证明:△ACD与△CBE全等.
理由如下:∵AD⊥直线l,
∴∠DAC+∠ACD=90°,
∵∠ACB=90°,
∴∠BCE+∠ACD=90°,
∴∠DAC=∠ECB,
在△ACD和△CBE中,
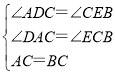 ,
,
∴△ACD≌△CBE(AAS);
(2)解:①由题意得,AM=t,FN=3t,
则CM=8-t,
由折叠的性质可知,CF=CB=6,
∴CN=6-3t;
②由折叠的性质可知,∠BCE=∠FCE,
∵∠MCD+∠CMD=90°,∠MCD+∠BCE=90°,
∴∠NCE=∠CMD,
∴当CM=CN时,△MDC与△CEN全等,
当点F沿F→C路径运动时,8-t=6-3t,
解得,t=-1(不合题意),
当点F沿C→B路径运动时,8-t═3t-6,
解得,t=3.5,
当点F沿B→C路径运动时,由题意得,8-t=18-3t,
解得,t=5,
当点F沿C→F路径运动时,由题意得,8-t=3t-18,
解得,t=6.5,
综上所述,当t=3.5秒或5秒或6.5秒时,△MDC与△CEN全等.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
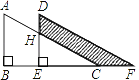
【题目】如图,两个大小一样的直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,AB=10,DH=4,平移距离为6,则阴影部分面积是_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知射线![]() 与直线
与直线![]() 交于点
交于点![]() ,
,![]() 平分
平分![]() ,
,![]() 于点
于点![]() ,
,![]() .
.
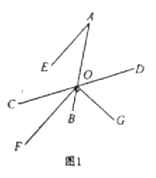
(1)如图1,若![]() ;
;
①求![]() 的度数;
的度数;
②试说明![]() 平分
平分![]() .
.
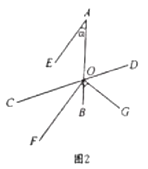
(2)如图2,设![]() 的度数为
的度数为![]() ,当为多少度时,射线
,当为多少度时,射线![]() 是
是![]() 的三等分线?并说明理由.
的三等分线?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】绿豆在相同条件下的发芽试验,结果如下表所示:
每批 粒数n | 100 | 300 | 400 | 600 | 1000 | 2000 | 3000 |
发芽的 粒数m | 96 | 282 | 382 | 570 | 948 | 1912 | 2850 |
发芽的 频率 | 0.960 | 0.940 | 0.955 | 0.950 | 0.948 | 0.956 | 0.950 |
则绿豆发芽的概率估计值是( )
A. 0.96 B. 0.95 C. 0.94 D. 0.90
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图(1),已知:在等腰直角三角形![]() 中,
中,![]() ,直线
,直线![]() 经过点
经过点![]() ,
,![]() 直线
直线![]() ,
,![]() 直线
直线![]() ,垂足分别为点
,垂足分别为点![]() 、
、![]() .则
.则![]() 、
、![]() 和
和![]() 之间的数量关系是: .
之间的数量关系是: .
(2)如图(2),将(1)中的条件改为:在等腰三角形![]() 中,
中,![]() 、
、![]() 、
、![]() 三点都在直线
三点都在直线![]() 上,且
上,且![]() ,其中
,其中![]() 为任意锐角或钝角.请问结论
为任意锐角或钝角.请问结论![]() 是否成立?如成立,请你给出证明;若不成立,请说明理由.
是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),![]() 、
、![]() 是直线
是直线![]() 上的两动点(
上的两动点(![]() 、
、![]() 、
、![]() 三点互不重合),点
三点互不重合),点![]() 为
为![]() 平分线上的一点,且
平分线上的一点,且![]() 和
和![]() 均为等边三角形,连接
均为等边三角形,连接![]() 、
、![]() ,若
,若![]() ,求证:
,求证:![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两地相距600千米,甲、乙两车同时从A地出发驶向B地,甲车到达B地后立即返回,它们各自离A地的距离y(千米)与行驶时间x(时)之间的函数关系图象如图所示.
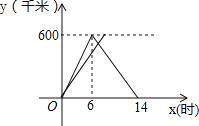
(1)求甲车行驶过程中y与x之间的函数关系式;
(2)当它们行驶了7小时时,两车相遇,求乙车的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在10×10的正方形网格中,每个小正方形的边长为1个单位长度.△ABC的顶点都在正方形网格的格点上,且通过两次平移(沿网格线方向作上下或左右平移)后得到△A'B'C',点C的对应点是直线上的格点C'.
(1)画出△A'B'C'.
(2)若连接AA′、BB′,则这两条线段之间的关系是 .
(3)试在直线l上画出格点P,使得由点A'、B'、C'、P四点围成的四边形的面积为9.
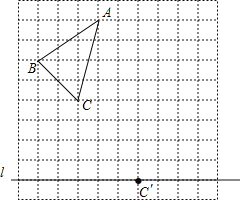
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com