
【题目】A、B两地相距600千米,甲、乙两车同时从A地出发驶向B地,甲车到达B地后立即返回,它们各自离A地的距离y(千米)与行驶时间x(时)之间的函数关系图象如图所示.
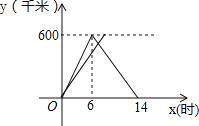
(1)求甲车行驶过程中y与x之间的函数关系式;
(2)当它们行驶了7小时时,两车相遇,求乙车的速度.
【答案】(1)y=![]() ;(2)乙车的速度为75千米/时.
;(2)乙车的速度为75千米/时.
【解析】
(1)根据函数图象可以得到甲车行驶过程中y与x之间的函数关系式;
(2)根据(1)求得函数解析式,可以得到当x=7时的y值,然后用求得的y值除以7即可求得乙车的速度.
解:(1)当0≤x≤6时,设甲车行驶过程中y与x之间的函数关系式为y=mx,
把(6,600)代入y=mx,
6m=600,
解得m=100,
∴y=100x;
当6<x≤14时,设甲车行驶过程中y与x之间的函数关系式为y=kx+b,
把(6,600)、(14,0)代入y=kx+b,
得![]() ,
,
解得,![]() ,
,
∴y=﹣75x+1050;
即甲车行驶过程中y与x之间的函数关系式为:y=![]() ;
;
(2)当x=7时,y=﹣75x+1050
解得,y=﹣75×7+1050=525,
525÷7=75(千米/时),
即乙车的速度为75千米/时.


 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
【题目】已知A、B两地相距300千米,甲、乙两车同时从A地出发,以各自的速度匀速向B地行驶.甲车先到达B地,停留1小时后,速度不变,按原路返回.设两车行驶的时间是x小时,离开A地的距离是y千米,如图是y与x的函数图象.
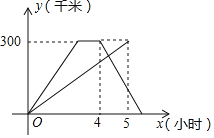
(1)甲车的速度是 ,乙车的速度是 ;
(2)甲车在返程途中,两车相距20千米时,求乙车行驶的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题情境】
如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.

【探究展示】
(1)证明:AM=AD+MC;
(2)AM=DE+BM是否成立?若成立,请给出证明;若不成立,请说明理由.
【拓展延伸】
(3)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,探究展示(1)、(2)中的结论是否成立?请分别作出判断,不需要证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直角三角形![]() 中,
中,![]() ,直线
,直线![]() 过点
过点![]() .
.
(1)当![]() 时,如图①,分别过点
时,如图①,分别过点![]() 、
、![]() 作
作![]() 于点
于点![]() ,
,![]() 于点
于点![]() .求证:
.求证:![]() .
.
(2)当![]() ,
,![]() 时,如图②,点
时,如图②,点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,连接
对称,连接![]() 、
、![]() ,动点
,动点![]() 从点
从点![]() 出发,以每秒1个单位长度的速度沿
出发,以每秒1个单位长度的速度沿![]() 边向终点
边向终点![]() 运动,同时动点
运动,同时动点![]() 从点
从点![]() 出发,以每秒3个单位的速度沿
出发,以每秒3个单位的速度沿![]() 向终点
向终点![]() 运动,点
运动,点![]() 、
、![]() 到达相应的终点时停止运动,过点
到达相应的终点时停止运动,过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,设运动时间为
,设运动时间为![]() 秒.
秒.
①用含![]() 的代数式表示
的代数式表示![]() .
.
②直接写出当![]() 与
与![]() 全等时
全等时![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图锐角△ABC,若∠ABC=40°,∠ACB=70°,点D、E在边AB、AC上,CD与BE交于点H.
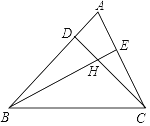
(1)若BE⊥AC,CD⊥AB,求∠BHC的度数.
(2)若BE、CD平分∠ABC和∠ACB,求∠BHC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一元二次方程mx2-2mx+m-2=0.
(1)若方程有两个不等实数根,求m的取值范围;
(2)若方程的两实数根为x1,x2,且|x1-x2|=1,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道“两边和一角分别相等的两个三角形不一定全等”,如图(1),![]() ,
,![]() ,
,![]() ,但
,但![]() 与
与![]() 却不全等.但是如果两个直角三角形呢?如图(2)
却不全等.但是如果两个直角三角形呢?如图(2)![]() ,
,![]() ,
,![]() ,则
,则![]() 吗?
吗?

(1)根据图(2)完成以下证明和阅读:
![]() 和
和![]() 中,
中,![]()
![]() ,
,![]() ____________(勾股定理)
____________(勾股定理)
![]() ,
,![]() ____________
____________
![]() ,
,![]() .
.![]() ____________
____________
在![]() 与
与![]() 中,
中,![]() ,
,![]() ,
,![]()
![]() ____________(____________)
____________(____________)
归纳:斜边和一条直角边相等的两个直角三角形全等;简称为“斜边直角边”或“![]() ”.
”.
几何语言如下:
在![]() 与
与![]() 中,
中,![]()
![]() ,
,![]()
![]()
(2)如图(3)已知![]() ,
,![]() ;求证:
;求证:![]() 平分
平分![]() .(每一步都要填写理由)
.(每一步都要填写理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地相距80km,一辆汽车上午9:00从甲地出发驶往乙地,匀速行驶了一半的路程后将速度提高了20km/h,并继续匀速行驶至乙地,汽车行驶的路程y(km)与时间x(h)之间的函数关系如图所示,该车到达乙地的时间是当天上午( )
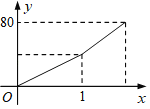
A. 10:35 B. 10:40 C. 10:45 D. 10:50
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com