
【题目】我们知道“两边和一角分别相等的两个三角形不一定全等”,如图(1),![]() ,
,![]() ,
,![]() ,但
,但![]() 与
与![]() 却不全等.但是如果两个直角三角形呢?如图(2)
却不全等.但是如果两个直角三角形呢?如图(2)![]() ,
,![]() ,
,![]() ,则
,则![]() 吗?
吗?

(1)根据图(2)完成以下证明和阅读:
![]() 和
和![]() 中,
中,![]()
![]() ,
,![]() ____________(勾股定理)
____________(勾股定理)
![]() ,
,![]() ____________
____________
![]() ,
,![]() .
.![]() ____________
____________
在![]() 与
与![]() 中,
中,![]() ,
,![]() ,
,![]()
![]() ____________(____________)
____________(____________)
归纳:斜边和一条直角边相等的两个直角三角形全等;简称为“斜边直角边”或“![]() ”.
”.
几何语言如下:
在![]() 与
与![]() 中,
中,![]()
![]() ,
,![]()
![]()
(2)如图(3)已知![]() ,
,![]() ;求证:
;求证:![]() 平分
平分![]() .(每一步都要填写理由)
.(每一步都要填写理由)
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案科目:初中数学 来源: 题型:
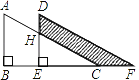
【题目】如图,两个大小一样的直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,AB=10,DH=4,平移距离为6,则阴影部分面积是_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两地相距600千米,甲、乙两车同时从A地出发驶向B地,甲车到达B地后立即返回,它们各自离A地的距离y(千米)与行驶时间x(时)之间的函数关系图象如图所示.
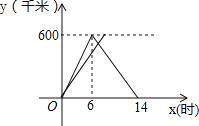
(1)求甲车行驶过程中y与x之间的函数关系式;
(2)当它们行驶了7小时时,两车相遇,求乙车的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
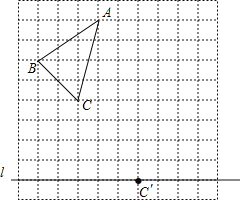
【题目】如图,在10×10的正方形网格中,每个小正方形的边长为1个单位长度.△ABC的顶点都在正方形网格的格点上,且通过两次平移(沿网格线方向作上下或左右平移)后得到△A'B'C',点C的对应点是直线上的格点C'.
(1)画出△A'B'C'.
(2)若连接AA′、BB′,则这两条线段之间的关系是 .
(3)试在直线l上画出格点P,使得由点A'、B'、C'、P四点围成的四边形的面积为9.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分8分)
如图,用两段等长的铁丝恰好可以分别围成一个正五边形和一个正六边形,其中正五边形的边长为(![]() )
)![]() ,正六边形的边长为(
,正六边形的边长为(![]() )cm(其中
)cm(其中![]() ),求这两段铁丝的总长
),求这两段铁丝的总长

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人用手指玩游戏,规则如下:i)每次游戏时,两人同时随机地各伸出一根手指;ii)两人伸出的手指中,大拇指只胜食指,食指只胜中指,中指只胜无名指,无名指只胜小拇指,小拇指只胜大拇指,否则不分胜负,依据上述规则,当甲、乙两人同时随机地各伸出一根手指时,
(1)求甲伸出小拇指取胜的概率;
(2)求乙取胜的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
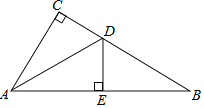
【题目】如图,在Rt△ABC中,∠C=90°.AD是△ABC的角平分线,若CD=4,AC=12,AB=15,DE⊥AB于E,则△BDE的面积是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李明准备进行如下操作实验,把一根长40 cm的铁丝剪成两段,并把每段首尾相连各围成一个正方形.
(1)要使这两个正方形的面积之和等于58 cm2,李明应该怎么剪这根铁丝?
(2)李明认为这两个正方形的面积之和不可能等于48 cm2,你认为他的说法正确吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com