
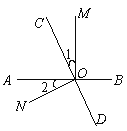
【题目】如图,直线AB,CD相交于O点,OM⊥AB.
(1)若∠1=∠2,求∠NOD;
(2)若∠1=![]() ∠BOC,求∠AOC与∠MOD.
∠BOC,求∠AOC与∠MOD.
【答案】(1)90°;(2)∠AOC=60°,∠MOD=150°.
【解析】(1)根据垂直的定义,可得∠AOC+∠1=90°由此易推出∠CON=90°,进而结合平角的定义即可解答本题;
(2)根据垂直可知∠AOM=∠BOM=90°,结合∠1=![]() ∠BOC,可得∠1=30°,由此可以得到∠AOC与MOD的度数.
∠BOC,可得∠1=30°,由此可以得到∠AOC与MOD的度数.
解:(1)∵OM⊥AB,
∴∠AOM=90°,即∠AOC+∠1=90°.
∵∠1=∠2,∠AOC+∠1=90°,
∴∠AOC+∠2=90°,
即∠CON=90°,
∵∠CON+∠NOD=180°,
∴∠NOD=90°.
(2)∵OM⊥AB,
∴∠AOM=∠BOM=90°.
∵∠BOC=∠BOM+∠1,∠BOM=90°,∠1=![]() ∠BOC,
∠BOC,
∴∠1=30°.
∵∠AOC+∠1=∠AOM=90°,∠1=30°,
∴∠AOC=60°,
∴∠BOD=∠AOC=60°,
∴∠MOD=∠MOB+∠AOC=150°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知直线a,b,c,d,e,且∠1=∠2,∠3=∠4,则a与c平行吗?为什么?
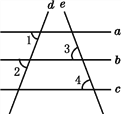
解:a与c平行;
理由:因为∠1=∠2 (_________________)
所以a//b (__________________________________________)
因为∠3=∠4 (_________________)
所以b//c (__________________________________________)
所以a//c (__________________________________________)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C为⊙O上一点,AD⊥CD,(点D在⊙O外)AC平分∠BAD.

(1)求证:CD是⊙O的切线;
(2)若DC、AB的延长线相交于点E,且DE=12,AD=9,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从A地到B地的公路需经过C地,图中AC=10千米,∠CAB=25°,∠CBA=37°. 因城市规划的需要,将在A、B两地之间修建一条笔直的公路.
(1)求改直后的公路AB的长;
(2)问公路改直后该段路程比原来缩短了多少千米?(sin25°≈0.42,cos25°≈0.91,sin37°≈0.60,tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为点F,则EF的长为( ) 
A.1
B.4﹣2 ![]()
C.![]()
D.3 ![]() ﹣4
﹣4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com