练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，四边形ABCD是边长为1的正方形，P是ABCD的边CD上的任意一点，且PE⊥DB于点E，PF⊥AC于点F，则PE+PF= ．

    【答案】
    【解析】解：ABCD是正方形，则OA=OD，AO⊥BD 连接OP，易得S△AOD=S△AOP=S△ODP；即 OAPE+ ODPF= ODAO，
    ∴PE+PF=AE；
    在Rt△ABD中，根据勾股定理就易得BD= ．
    根据△ABD的面积= ABAD= BDAE；
    解得AE= ，则PE+PF= ．
    故答案为 ．
    根据正方形的性质，对角线相等且互相平分，因而得到：OA=OD，AO⊥BD连接OP，根据△AOD的面积等于△AOP的面积等于△ODP的面积．得到关系式；进而根据勾股定理就可以求出BD的长．根据△ABD的面积= ABAD= BDAE；解可得AE的值，进而可得PE+PF的值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知|a+3|+|b﹣1|=0，则ab的值是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小张骑自行车匀速从甲地到乙地，在途中休息了一段时间后，仍按原速行驶.他距乙地的距离y（km）与时间x(h)的关系如图中折线所示，小李开车匀速从乙地到甲地，比小张晚出发一段时间，他距乙地的距离y(km)与时间x(h)的关系如图中线段ＡＢ所示．

    (1)小李到达甲地后，再经过_______小时小张也到达乙地；小张骑自行车的速度是_______千米／小时.

    (2)小张出发几小时与小李相距15千米？

    (3)若小李想在小张休息期间与他相遇，则他出发的时间x应在什么范围？（直接写出答案）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

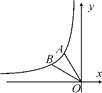
    【题目】如图，已知反比例函数y＝的图象经过点A(－1， )．

    (1)试确定此反比例函数的解析式；

    (2)点O是坐标原点，将线段OA绕点O逆时针旋转30°后得到线段OB，求出点B的坐标，并判断点B是否在此反比例函数的图象上．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】点A(a,b)和点B关于x轴对称,而点B与点C(2,3)关于y轴对称,那么a=__,b=__,点A和点C的位置关系是__.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图四边形ABCD是一块草坪，量得四边长AB=3m，BC=4m，DC=12m，AD=13m，∠B=90°，求这块草坪的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列事件中是必然发生的事件是（　 　）

    A.投掷一枚质地均匀的骰子，掷得的点数是奇数；

    B.某种彩票中奖率是1%，则买这种彩票100张一定会中奖；

    C.掷一枚硬币，正面朝上 ；

    D.任意画一个三角形，其内角和是180° ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图,已知直线a,b,c,d,e,且∠1=∠2,∠3=∠4,则a与c平行吗?为什么?

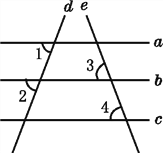
    解:a与c平行.

    理由:因为∠1=∠2(_________________),

    所以a∥b(_________________).

    因为∠3=∠4(_________________),

    所以b∥c(_________________).

    所以a∥c(_________________).

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图,直线AB，CD相交于O点，OM⊥AB.

    （1）若∠1=∠2，求∠NOD；

    （2）若∠1=∠BOC，求∠AOC与∠MOD.

    查看答案和解析>>

    同步练习册答案