
【题目】如图,AB是⊙O的直径,C为⊙O上一点,AD⊥CD,(点D在⊙O外)AC平分∠BAD.

(1)求证:CD是⊙O的切线;
(2)若DC、AB的延长线相交于点E,且DE=12,AD=9,求BE的长.
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)连接OC,根据条件先证明OC∥AD,然后证出OC⊥CD即可;(2)先利用勾股定理求出AE的长,再根据条件证明△ECO∽△EDA,然后利用对应边成比例求出OC的长,再根据BE=AE﹣2OC计算即可.
试题解析:(1)证明:连接OC,

∵AC平分∠DAB,
∴∠DAC=∠CAB,
∵OC=OA,
∴∠OAC=∠OCA,
∴∠DAC=∠OCA,
∴OC∥AD,
∵AD⊥CD,
∴OC⊥CD,
∵OC为⊙O半径,
∴CD是⊙O的切线.
(2)解:在Rt△ADE中,由勾股定理得:AE=![]() =15,
=15,
∵OC∥AD,
∴△ECO∽△EDA,
∴![]()
∴![]()
解得:OC=![]() ,
,
∴BE=AE﹣2OC=15﹣2×![]() =
=![]() ,
,
答:BE的长是![]() .
.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】地球上的海洋面积约为361000000km2 , 这个数用科学记数法表示为( )km2 .
A.361×106
B.36.1×107
C.3.61×108
D.0.361×109
查看答案和解析>>
科目:初中数学 来源: 题型:
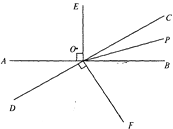
【题目】.如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OE⊥AB,OF⊥CD,
(1)图中除直角外,还有相等的角吗?请写出两对:①____________;②____________.
(2)如果∠AOD=40°,则①∠BOC=_______;②OP是∠BOC的平分线,所以∠COP=______度;
③求∠BOF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验初中组织了“英语手抄报”征集活动,现从中随机抽取部分作品,按A、B、C、D四个等级进行评价,并根据统计结果绘制了如下两幅不完整的统计图.

(1)抽取了_____份作品;
(2)此次抽取的作品中等级为B的作品有______份,并补全条形统计图;
(3)若该校共征集到600份作品,请估计等级为A的作品约有多少份?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点M,N.当∠MAN绕点A旋转到BM=DN时(如图1),易证BM+DN=MN.

(1)当∠MAN绕点A旋转到BM≠DN时(如图2),线段BM,DN和MN之间有怎样的数量关系?写出猜想,并加以证明.
(2)当∠MAN绕点A旋转到如图3的位置时,线段BM,DN和MN之间又有怎样的数量关系?请直接写出你的猜想.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com