
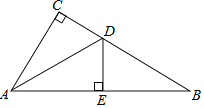
【题目】如图,在Rt△ABC中,∠C=90°.AD是△ABC的角平分线,若CD=4,AC=12,AB=15,DE⊥AB于E,则△BDE的面积是______.
 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
【题目】【问题情境】
如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.

【探究展示】
(1)证明:AM=AD+MC;
(2)AM=DE+BM是否成立?若成立,请给出证明;若不成立,请说明理由.
【拓展延伸】
(3)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,探究展示(1)、(2)中的结论是否成立?请分别作出判断,不需要证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道“两边和一角分别相等的两个三角形不一定全等”,如图(1),![]() ,
,![]() ,
,![]() ,但
,但![]() 与
与![]() 却不全等.但是如果两个直角三角形呢?如图(2)
却不全等.但是如果两个直角三角形呢?如图(2)![]() ,
,![]() ,
,![]() ,则
,则![]() 吗?
吗?

(1)根据图(2)完成以下证明和阅读:
![]() 和
和![]() 中,
中,![]()
![]() ,
,![]() ____________(勾股定理)
____________(勾股定理)
![]() ,
,![]() ____________
____________
![]() ,
,![]() .
.![]() ____________
____________
在![]() 与
与![]() 中,
中,![]() ,
,![]() ,
,![]()
![]() ____________(____________)
____________(____________)
归纳:斜边和一条直角边相等的两个直角三角形全等;简称为“斜边直角边”或“![]() ”.
”.
几何语言如下:
在![]() 与
与![]() 中,
中,![]()
![]() ,
,![]()
![]()
(2)如图(3)已知![]() ,
,![]() ;求证:
;求证:![]() 平分
平分![]() .(每一步都要填写理由)
.(每一步都要填写理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只渔船在灯塔C的正西方向10海里的A处,以20海里/时的速度沿北偏东30°方向行驶.
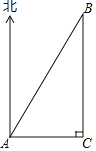
(1)多长时间后,渔船距灯塔最近?
(2)多长时间后,渔船行驶到灯塔的正北方向?此时渔船距灯塔有多远?(其中:202-102=17.32)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个转盘被平均分成12份,每份上写上不同的数字,游戏方法:先猜数后转动转盘,若指针指向的数字与所猜的数一致,则猜数者获胜.现提供三种猜数方法:
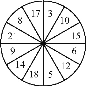
①猜是“奇数”,或是“偶数”;
②猜是“大于10的数”,或是“不大于10的数”;
③猜是“3的倍数”,或是“不是3的倍数”.
如果你是猜数者,你愿意选择哪一种猜数方法?怎样猜?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市开展“美丽泰安,创卫同行”活动,某校倡议学生利用双休日在某公园参加义务劳动,为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制了不完整的统计图,根据图中信息可知扇形图中的“1.5小时”部分圆心角的度数是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地相距80km,一辆汽车上午9:00从甲地出发驶往乙地,匀速行驶了一半的路程后将速度提高了20km/h,并继续匀速行驶至乙地,汽车行驶的路程y(km)与时间x(h)之间的函数关系如图所示,该车到达乙地的时间是当天上午( )
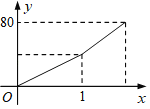
A. 10:35 B. 10:40 C. 10:45 D. 10:50
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com