
【题目】如图,正方形ABCD的边长为3,E,F 分别是AB,BC边上的点,且∠EDF=45°.将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)求证:EF=FM;
(2)当AE=1时,求EF的长.

【答案】(1)证明见解析(2)![]()
【解析】试题分析:(1)由旋转的性质可知,DE=DM,∠EDM=90°,因为∠EDF=45°,所以∠FDM=∠EDM=45°,通过证明△DEF≌△DMF得到EF=MF;
(2)设EF=MF=x,则BF=4-x,BE=2,在Rt△EBF中,由勾股定理得到关于x的等式,解得x的值即可.
试题解析:(1)证明:∵△DAE逆时针旋转90°得到△DCM,
∴DE=DM,∠EDM=90°,
∴∠EDF+∠FDM=90°,
∵∠EDF=45°,
∴∠FDM=∠EDM=45°,
在△DEF和△DMF中,
DE=DM,∠EDF=∠MDF,DF=DF,
∴△DEF≌△DMF(SAS),
∴EF=MF;
(2)设EF=MF=x, ∵AE=CM=1,且BC=3,
∴BM=BC+CM=3+1=4,
∴BF=BM-MF=BM-EF=4-x,
∵EB=AB-AE=3-1=2,
在Rt△EBF中,由勾股定理得EB+BF=EF, 即2+(4-x)=x,
解得:x=![]() , 则EF=
, 则EF=![]() .
.


科目:初中数学 来源: 题型:
【题目】我国总人口数约为1370000000人,1370000000这个数用科学记数法表示正确的是( )
A. 137×107B. 13.7×108C. 1.37×109D. 0.137×1010
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正三角形ABC内接于⊙O,P是BC上的一点,且PB<PC,PA交BC于E,点F是PC延长线上的点,CF=PB,AB=![]() ,PA=4.
,PA=4.
(1)求证:△ABP≌△ACF;
(2)求证:AC2=PAAE;
(3)求PB和PC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知空气的单位体积质量是0.001239g/cm3,则用科学记数法表示该数为( )
A. 1.239×10﹣3g/cm3 B. 1.239×10﹣2g/cm3
C. 0.1239×10﹣2g/cm3 D. 12.39×10﹣4g/cm3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列计算:①a2nan=a3n;②2233=65;③32÷32=1;④a3÷a2=5a;⑤(﹣a)2(﹣a)3=a5.其中正确的式子有( )
A. 4 个 B. 3 个 C. 2 个 D. 1 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC中,AC=BC=10,AB=12.
(1)动手操作:利用尺规作以BC为直径的⊙O,⊙O交AB于点D,⊙O交AC于点E,并且过点D作DF⊥AC交AC于点F.
(2)求证:直线DF是⊙O的切线;
(3)连接DE,记△ADE的面积为S1,四边形DECB的面积为S2,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线MN与x轴,y轴分别相交A、C两点,分别过A、C作x轴、y轴的垂线,二者相交于B点,且OA=8,OC=6.
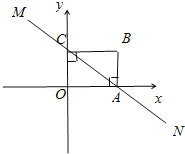
(1)求直线MN的解析式;
(2)已知在直线MN上存在点P,使△PBC是等腰三角形,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com