
【题目】如图,等腰三角形ABC中,AC=BC=10,AB=12.
(1)动手操作:利用尺规作以BC为直径的⊙O,⊙O交AB于点D,⊙O交AC于点E,并且过点D作DF⊥AC交AC于点F.
(2)求证:直线DF是⊙O的切线;
(3)连接DE,记△ADE的面积为S1,四边形DECB的面积为S2,求![]() 的值.
的值.

【答案】(1)作图见解析;(2)证明见解析;(3)![]() =
=![]() .
.
【解析】试题分析:(1)根据题意作出图形即可;
(2)连接OD,根据等腰三角形的性质得到∠A=∠ODB根据平行线的判定得到OD∥AC,由平行线的性质得到∠ODF=∠AFD=90°,于是得到结论;
(3)连接DE;根据圆周角定理得到∠CDB=90°,即CD⊥AB,由等腰三角形的性质得到AD=BD=![]() AB=6,根据圆内接四边形的性质得到∠BDE+∠C=180°,等量代换得到∠C=∠ADE,根据相似三角形的性质得到
AB=6,根据圆内接四边形的性质得到∠BDE+∠C=180°,等量代换得到∠C=∠ADE,根据相似三角形的性质得到![]() ,于是得到结论.
,于是得到结论.
试题解析:(1)如图所示,图形为所求;
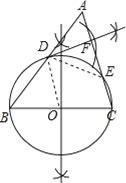
(2)连接OD
∵DF⊥AC,∴∠AFD=90°,
∵AC=BC∴∠A=∠B,
∵OB=OD,∴∠B=∠ODB,∴∠A=∠ODB∴OD∥AC,
∴∠ODF=∠AFD=90°,∴直线DF是⊙O的切线;
(3)连接DE;
∵BC是⊙O的直径,∴∠CDB=90°,即CD⊥AB,
∵AC=BC,CD⊥AB,∴AD=BD=![]() AB=6,
AB=6,
∵四边形DECB是圆内接四边形,∴∠BDE+∠C=180°,
∵∠BDE+∠ADE=180°,∴∠C=∠ADE,
∵在△ADE和△ACB中,∠ADE=∠C,∠DAE=∠CAB,
∴△ADE∽△ACB,∴![]() ,∴
,∴![]() ,
,
∵S△ABC=S△ADE+S四边形DECB,∴![]() ,
,
∴![]() ,即
,即![]() =
=![]() .
.


 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为3,E,F 分别是AB,BC边上的点,且∠EDF=45°.将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)求证:EF=FM;
(2)当AE=1时,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将点M向左平移3个单位长度后的坐标是(-2,1),则点M的坐标是( )
A. (-2,4)B. (-5,1)C. (1,1)D. (-2,-4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年4月21日在深圳体育馆召开的第八届中国(深圳)国际茶业文化博览会上某茶商将甲、乙两种茶叶卖出,甲种茶叶卖出1200元,盈利20%,乙种茶叶卖出1200元,亏损20%,则此人在这次交易中是( )
A.盈利50元
B.盈利100元
C.亏损150元
D.亏损100元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y= ![]() 过点A(2,4),B(0,3)、题目中的矩形部分是一段因墨水污染而无法辨认的文字.
过点A(2,4),B(0,3)、题目中的矩形部分是一段因墨水污染而无法辨认的文字.
(1)根据现有的信息,请求出题中的一次函数的解析式.
(2)根据关系式画出这个函数图象.
(3)过点B能不能画出一直线BC将△ABO(O为坐标原点)分成面积比为1:2的两部分?如能,可以画出几条,并求出其中一条直线所对应的函数关系式,其它的直接写出函数关系式;若不能,说明理由.
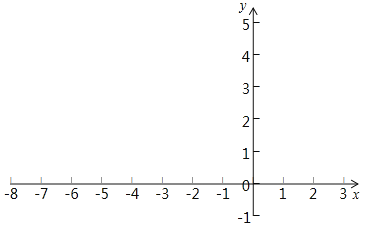
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com