
【题目】已知一次函数y= ![]() 过点A(2,4),B(0,3)、题目中的矩形部分是一段因墨水污染而无法辨认的文字.
过点A(2,4),B(0,3)、题目中的矩形部分是一段因墨水污染而无法辨认的文字.
(1)根据现有的信息,请求出题中的一次函数的解析式.
(2)根据关系式画出这个函数图象.
(3)过点B能不能画出一直线BC将△ABO(O为坐标原点)分成面积比为1:2的两部分?如能,可以画出几条,并求出其中一条直线所对应的函数关系式,其它的直接写出函数关系式;若不能,说明理由.
【答案】(1) y=0.5x+3.(2)作图见解析;(3)y=-2.5x+3或y=-0.25x+3.
【解析】试题分析:(1)设一次函数的解析式是y=kx+b,把A(0,3)、B(2,4)代入得出方程组,求出方程组的解即可;
(2)过A、B作直线即可;
(3)根据面积得出C、C′点,求出直线AO的解析式,根据A的坐标求出C和C′的坐标,设直线BC的解析式,把B、C(或)C′的坐标代入求出即可.
试题解析:(1)解:设一次函数的解析式是y=kx+b,
∵把A(0,3)、B(2,4)代入得:
![]() ,解得:k=0.5,b=3,
,解得:k=0.5,b=3,
∴一次函数的解析式是y=0.5x+3.
(2)解:如图.
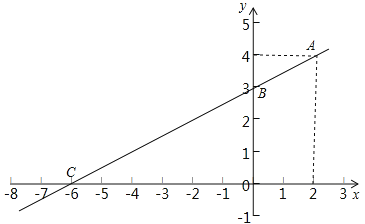
(3)解:能,有两条,如图:
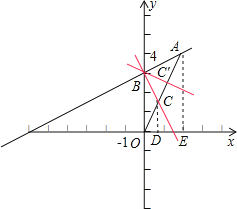
直线BC和BC′都符合题意,
OC=CC′=AC′,
则C的纵坐标是![]() ×4=
×4=![]() ,
,
C′的纵坐标是![]() ×4=
×4= ![]() ,
,
设直线OA的解析式是y=kx,
把A(2,4)代入得:k=2,
∴y=2x,
把C、C′的纵坐标代入得出C的横坐标是![]() ,C′的横坐标是
,C′的横坐标是![]() ,
,
∴C(![]() ,
,![]() ),C′(
),C′(![]() ,
,![]() ),
),
设直线BC的解析式是y=kx+3,
把C的坐标代入得:k=-2.5,
∴直线BC的解析式是y=-2.5x+3,
同理求出直线BC′的解析式是y=-0.25x+3,
即过点B能画出直线BC将△ABO(O为坐标原点)分成面积比为1:2的两部分,可以画出2条,直线所对应的函数关系式是y=-2.5x+3或y=-0.25x+3.


科目:初中数学 来源: 题型:
【题目】我国总人口数约为1370000000人,1370000000这个数用科学记数法表示正确的是( )
A. 137×107B. 13.7×108C. 1.37×109D. 0.137×1010
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC中,AC=BC=10,AB=12.
(1)动手操作:利用尺规作以BC为直径的⊙O,⊙O交AB于点D,⊙O交AC于点E,并且过点D作DF⊥AC交AC于点F.
(2)求证:直线DF是⊙O的切线;
(3)连接DE,记△ADE的面积为S1,四边形DECB的面积为S2,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线MN与x轴,y轴分别相交A、C两点,分别过A、C作x轴、y轴的垂线,二者相交于B点,且OA=8,OC=6.
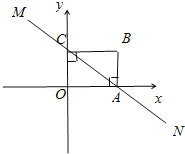
(1)求直线MN的解析式;
(2)已知在直线MN上存在点P,使△PBC是等腰三角形,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在x轴的上方,直角∠BOA绕原点O按顺时针方向旋转,若∠BOA的两边分别与函数y=﹣![]() 、y=
、y=![]() 的图象交于B、A两点,则∠OAB的大小的变化趋势为( )
的图象交于B、A两点,则∠OAB的大小的变化趋势为( )

A. 逐渐变小B.逐渐变大C.无法确定D.保持不变
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】荆州古城是闻名遐迩的历史文化名城,下表是荆州古城某历史景点一周的抽样统计参观人数,图20-3-5是门票价格统计.
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
人数 | 100 | 120 | 100 | 100 | 160 | 230 | 240 |
(1)把上表中一周的参观人数作为一个样本,直接指出这个样本的中位数,众数和平均数,分析表中数据还可得到一些信息,如双休日参观人数远远高于平时等,尝试再写出两条相关信息.
(2)若“五一”黄金周有甲、乙两旅行团到该景点参观,两团人数之和恰为上述样本数 据的中位数,乙团不超过50人,设两团分别购票共付W元,甲团人数x人.①求W与x的函数关系式;②若甲团人数不超过100人,说明两团合起来购票比分开购票最多可节约多少元?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com