Question

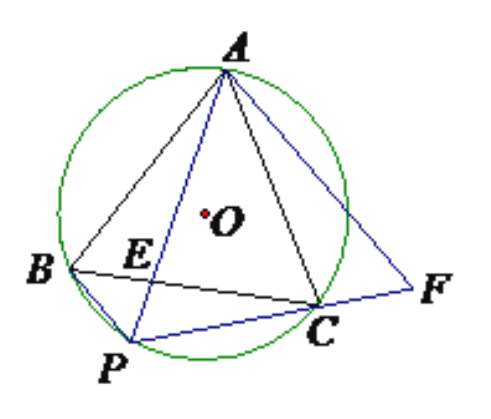
【题目】如图，正三角形ABC内接于⊙O，P是BC上的一点，且PB＜PC，PA交BC于E，点F是PC延长线上的点，CF=PB，AB=，PA=4．

（1）求证：△ABP≌△ACF；

（2）求证：AC2=PAAE；

（3）求PB和PC的长．

Answer 1

【答案】（1）证明见解析；（2）证明见解析；（3）PB=1，PC=3．

【解析】试题分析：（1）先根据等边三角形的性质得到AB=AC，再利用圆的内接四边形的性质得∠ACF=∠ABP，于是可根据“SAS”判断△ABP≌△ACF；

（2）先根据等边三角形的性质得到∠ABC=∠ACB=60°，再根据圆周角定理得∠APC=∠ABB=60°，加上∠CAE=∠PAC，于是可判断△ACE∽△APC，然后利用相似比即可得到结论；

（3）先利用AC2=PAAE计算出AE= ，则PE=AP-AE= ，再证△APF为等边三角形，得到PF=PA=4，则有PC+PB=4，接着证明△ABP∽△CEP，得到PBPC=PEA=3，然后根据根与系数的关系，可把PB和PC看作方程x2-4x+3=0的两实数解，再解此方程即可得到PB和PC的长．

试题解析：

（1）∵∠ACP+∠ABP=180°，

又∠ACP+∠ACF=180°，

∴∠ABP=∠ACF

在和中，

∵AB=AC，∠ABP=∠ACF，

∴≌．

(2)在和中，

∵∠APC=∠ABC，

而是等边三角形，故∠ACB=∠ABC=60，

∴∠ACE =∠APC .

又∠CAE =∠PAC ，

∴∽

∴,即.

由（1）知≌，

∴∠BAP=∠CAF，

∴∠BAP+∠PAC=∠CAF+∠PAC

∴∠PAF=∠BAC=60°，又∠APC＝∠ABC＝60°.

∴是等边三角形

∴AP=PF

∴

在与中，

∵∠BAP=∠ECP ，

又∠APB=∠EPC=60°，

∴∽

∴,即

由（2），

∴

∴

∴

因此PB和PC的长是方程的解．

解这个方程，得， ．

∵PB<PB，∴PB=，PC=，

∴PB和PC的长分别是1和3。