
在△ABC中,∠A=90°,AB=8,AC=6,M是AB上的动点(不与A,B重合),过M点作MN∥BC交AC于点N.以MN为直径作⊙O,并在⊙O内作内接矩形AMPN.
设AM=x.
(1)用含x的代数式表示△MNP的面积S;
(2)在动点M的运动过程中,记△MNP与梯形BCNM重合部分的面积为y,试求关于y的函数表达式,并求 x为何值时,y的值最大,最大值是多少?


(1) S=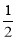 •x•
•x•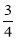 x=
x=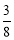 x2,(0<x≤8);(2) 当x=
x2,(0<x≤8);(2) 当x= 时,y有最大值,最大值为8.
时,y有最大值,最大值为8.
【解析】
试题分析:(1)先证明△AMN∽△ABC,则可根据相似三角形的对应边成比例求AN,然后由三角形的面积公式求得用x的代数式表示的△AMN的面积S;
(3)先求出P点在BC上时AM的值,然后进行讨论:当0<x≤4时,y=S=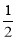 •x•
•x•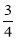 x=
x=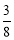 x2,根据二次函数的性质得到x=4,y的最大值为6;当4<x≤8时,PM与PN分别交BC于E、F,y=S梯形MEFN=S△PMN-S△PEF,利用矩形的性质可表示出PN=AM=x;再由平行四边形BFNM的性质解得FN=8-x,PF=2x-8,则可利用相似三角形Rt△PEF∽Rt△ABC的性质求得S△PEF值;然后写出y与x的解析式,再根据二次函数的性质求出y的最大值,最后综合两种情况即可.
x2,根据二次函数的性质得到x=4,y的最大值为6;当4<x≤8时,PM与PN分别交BC于E、F,y=S梯形MEFN=S△PMN-S△PEF,利用矩形的性质可表示出PN=AM=x;再由平行四边形BFNM的性质解得FN=8-x,PF=2x-8,则可利用相似三角形Rt△PEF∽Rt△ABC的性质求得S△PEF值;然后写出y与x的解析式,再根据二次函数的性质求出y的最大值,最后综合两种情况即可.
(1)∵MN∥BC,
∴△AMN∽△ABC,
∴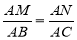 ,
,
即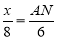 ,解得AN=
,解得AN=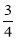 x,
x,
∴△AMN的面积=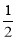 •x•
•x•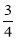 x=
x=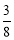 x2,
x2,
∵四边形AMPN是矩形,
∴S=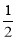 •x•
•x•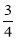 x=
x=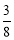 x2,(0<x≤8);
x2,(0<x≤8);
(2)若P点在BC上时,
∵四边形AMPN是矩形,
∴O点为AP的中点,
而MN∥BC,
∴MN为△ABC的中位线,此时AM=4,
当0<x≤4时,y=S=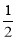 •x•
•x•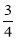 x=
x=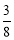 x2,此时x=4,y的最大值为6;
x2,此时x=4,y的最大值为6;
当4<x≤8时,PM与PN分别交BC于E、F,如图,
y=S梯形MEFN=S△PMN-S△PEF,
∵四边形AMPN是矩形,
∴PN=AM=x,
∵MN∥BC,
∴四边形BFNM是平行四边形,
∴FN=BM=8-x,PF=PN-FN=x-(8-x)=2x-8,
∵Rt△PEF∽Rt△ACB,
∴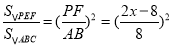 ,
,
而S△ABC=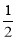 ×8×6=24,
×8×6=24,
∴S△PEF= (x-4)2,
(x-4)2,
∴y=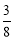 x2-
x2- (x-4)2
(x-4)2
=-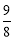 x2+12x-24,
x2+12x-24,
=-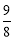 (x-
(x- )2+8(4<x≤8),
)2+8(4<x≤8),
∵a=-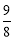 <0,
<0,
∴当x= 时,y有最大值,最大值为8,
时,y有最大值,最大值为8,
综上所述,当x= 时,y有最大值,最大值为8.
时,y有最大值,最大值为8.
考点:圆的综合题.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源:2013-2014学年安徽省当涂县四校九年级上学期期末联考数学试卷(解析版) 题型:解答题
如图所示,二次函数y=-x2+2x+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C.

(1)求m的值;
(2)求点B的坐标;
查看答案和解析>>
科目:初中数学 来源:2013-2014学年安徽十大名校九年级第四次月考数学试卷(解析版) 题型:选择题
下列运算正确的是
A.3a2-a2=3 B.(a2)3=a5 C.a3·a6=a9 D.(2a2)2=4a2
查看答案和解析>>
科目:初中数学 来源:2013-2014学年四川省眉山市华兴联谊学校九年级下学期期中考试数学试卷(解析版) 题型:选择题
一个多边形的内角和是外角和的2倍,则这个多边形的边数为( )
A、4 B、5 C、6 D、7
查看答案和解析>>
科目:初中数学 来源:2013-2014学年四川省眉山市华兴联谊学校九年级下学期期中考试数学试卷(解析版) 题型:选择题
下列运算结果正确的是( )
①2x3-x2= x ②x3·(x5)2=x13 ③(-x)6÷(-x)3=x3 ④(0.1)2·103=10
A、①② B、②④ C、②③ D、②③④
查看答案和解析>>
科目:初中数学 来源:2013-2014学年四川省乐山市夹江县九年级毕业会考适应性考试数学试卷(解析版) 题型:解答题
学习了统计知识后,小明就本班同学喜欢的体育 运动项目进行调查统计,如图是他通过收集数据绘制的两幅不完整的统计图.
(1)该班共有多少名学生;
(2)该班喜欢乒乓球的学生有多少名,并将条形统计图补充完整;
(3)若小明所在的年级共有500名学生,估计该年级喜欢乒乓球的学生多少名;
(4)在全班同学中随机选出一名学生,选出的学生恰好是喜欢篮球项目的概率是多少.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年四川省乐山市夹江县九年级毕业会考适应性考试数学试卷(解析版) 题型:填空题
如图,已知等腰梯形ABCD的底角∠B=45°,高AE=1,上底AD=1,则其面积为 .

查看答案和解析>>
科目:初中数学 来源:2013-2014学年吉林省长春市朝阳区中考一模数学试卷(解析版) 题型:解答题
一辆轿车从甲地驶往乙地,到达乙地后返回甲地,速度是原来的1.5倍,共用t小时;一辆货车同时从甲地驶往乙地,到达乙地后停止.两车同时出发,匀速行驶.设轿车行驶的时间为x(h),两车到甲地的距离为y(km),两车行驶过程中y与x之间的函数图象如图.
(1)求轿车从乙地返回甲地时的速度和t的值;
(2)求轿车从乙地返回甲地时y与x之间的函数关系式,并写出自变量x的取值范围;
(3)直接写出轿车从乙地返回甲地时与货车相遇的时间.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市顺义区中考二模数学试卷(解析版) 题型:选择题
从1,2,3这三个数字中随机抽取两个,抽取的这两个数的和是奇数的概率是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com