Question

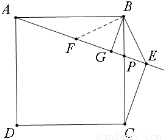
（本题8分）P是边长为4的正方形ABCD的边BC上任意一点，过B点作BG⊥AP于G，过C点作CE⊥AP于E，连BE.

（1）如图1，若P是BC的中点，求CE的长；

（2）如图2，当P在BC边上运动时，（不与B、C重合）求(AG-CE)/BE的值；

Answer 1

（1）CE=；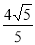

（2)；

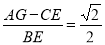【解析】

试题分析：(1)由勾股定理可求出AP的长,然后利用面积法即可求得BG的长,面由已知可证得CE=BG,从而可求；

（2）在AG上取一点F，使AF＝CE，然后证明△ABF≌△BCE，再证明△BGF是等腰直角三角形即可得到；

试题解析：（1）∵四边形ABCD是正方形

∴∠ABC=90°，AB=BC=4

∵P为BC中点

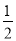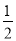∴BP=BC=×4=2

∴AP=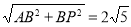

∵AB·BP=AP·BG

即4×2=BG

∴BG=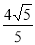

∵BG⊥AP，CE⊥AP

∴∠BGP=∠CEP=90°

又∵∠BPG=∠CPE，PB=PC

∴△BPG≌△CPE

∴CE=BG=；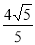

在AG上取一点F，使AF＝CE

∵ABCD是正方形

∴∠BAF＋∠APB＝90°

∵CE⊥PE

∴∠BCE＋∠CPE＝90°

而∠APB＝∠CPE

∴∠BAF＝∠BCE

又AB＝BC，AF＝CE

∴△ABF≌△BCE

∴BF＝CE，∠ABF＝∠CBE

由∠ABF＝∠CBE，∠ABC＝90°，得：∠EBF＝90°

由∠EBF＝90°，BF＝CE，得∠BFG＝45°，而BG⊥FG

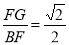∴，即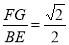

∵FG＝AG－AF＝AG－CE，

∴

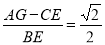
考点：1、勾股定理；2、三角形全等的判定与性质；3、等腰直角三角形的性质；4、正方形的性质

考点分析： 考点1：图形的相似 形状相同，大小不同的两个图形相似 试题属性

• 题型：
• 难度：
• 考核：
• 年级：