
式子 中x的取值范围是
中x的取值范围是
x≥1
【解析】
试题分析:由已知得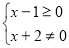 ,所以x≥1;
,所以x≥1;
考点:1、分式有意义的条件;2、二次根式有意义的条件
考点分析: 考点1:分式 分式:中考试题中分值约为6-8分,主要以填空,简答计算题型出现,难易度属于中。近几年主要考察①分式的概念,性质,意义②分式的运算,化简求值。③列分式方程解决实际问题、突破方法:①掌握并灵活应用分式的基本性质,②在通分和约分时,都要注意分解因式知识的应用。③化简求值时,注意整体思想和技巧的应用。④留意生活中是实际问题 考点2:二次根式 二次根式: 叫做二次根式。
叫做二次根式。 ”;
”; 有意义,被开方数a必须是非负数,即a≥0,由此可确定被开方数中字母的取值范围。
二次根式性质:
有意义,被开方数a必须是非负数,即a≥0,由此可确定被开方数中字母的取值范围。
二次根式性质: ≥0 (双重非负性 );
≥0 (双重非负性 ); ;
;
 ;
; 。
二次根式判定:
。
二次根式判定: ,
, 等;
等; 中,被开方数a可以是具体的一个数,也可以是代数式;
中,被开方数a可以是具体的一个数,也可以是代数式; 是一个非负数;
是一个非负数; (a≥0 )就表示a的算术平方根。
(a≥0 )就表示a的算术平方根。

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2014-2015学年浙江省台州市九年级上学期第一次月考数学试卷(解析版) 题型:选择题
已知二次函数的图象(0≤x≤3)如图所示,关于该函数在所给自变量取值范围内,下列说法正确的是( ).
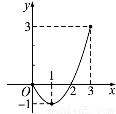
A.有最小值0,有最大值3 B.有最小值-1,有最大值0
C.有最小值-1,有最大值3 D.有最小值-1,无最大值
查看答案和解析>>
科目:初中数学 来源:2014-2015学年天津市九年级上学期期中考试数学试卷(解析版) 题型:填空题
如图,△ABC为等边三角形,D是△ABC 内一点,且AD=3,将△ABD绕点A旋转到△ACE的位置,连接DE,则DE的长为 .

查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省九年级上学期第一次月考数学试卷(解析版) 题型:解答题
(6分)南通百货大搂服装柜在销售中发现:“宝乐”牌童装平均每天可售出20件,每件盈利40元.元旦将至,商场决定采取适当的降价措施,扩大销售量,增加盈利,尽快减少库存.经市场调查发现:如果每件童装降价1元,那么平均每天就可多售出2件.要想平均每天销售这种童装盈利1200元,那么每件童装应降价多少元?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省九年级上学期第一次月考数学试卷(解析版) 题型:填空题
如图,四边形ABCD是菱形,AC、BD交于点O,DH⊥AB于H,连OH,若AC=8,OH=3,则AH=_________

查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省九年级上学期第一次月考数学试卷(解析版) 题型:选择题
如图,平行四边形ABCD的周长为20cm,AB≠AD,AC、BD相交于点0,EO⊥BD交AD于点E,则⊿ABE的周长为( )

A、4cm B、6cm C、8cm D、10cm
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省镇江市丹徒区九年级10月调研数学试卷(解析版) 题型:解答题
(8分) 我们用 表示不大于
表示不大于 的最大整数,例如:
的最大整数,例如: ,
, ,
, ;用
;用 表示大于
表示大于 的最小整数,例如:
的最小整数,例如: ,
, ,
, 。解决下列问题:
。解决下列问题:
(1) = ,
= , = .
= .
(2)若 =3则
=3则 的取值范围是 ;若
的取值范围是 ;若 =-2,则
=-2,则 的取值范围是 .
的取值范围是 .
(3)已知 ,
, 满足方程组
满足方程组 ,求
,求 ,
, 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省镇江市丹徒区九年级10月调研数学试卷(解析版) 题型:填空题
如图, 为等腰三角形,顶点
为等腰三角形,顶点 的坐标(2,
的坐标(2, ),底边OB在
),底边OB在 轴上.将
轴上.将 绕点
绕点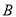 按顺时针方向旋转一定角度后得
按顺时针方向旋转一定角度后得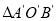 ,点
,点 的对应点
的对应点 在
在 轴上,则点
轴上,则点 的坐标为
的坐标为
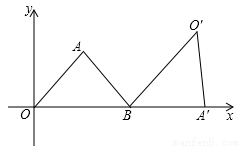
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省武汉市校九年级9月联考数学试卷(解析版) 题型:解答题
(本题8分)P是边长为4的正方形ABCD的边BC上任意一点,过B点作BG⊥AP于G,过C点作CE⊥AP于E,连BE.

(1)如图1,若P是BC的中点,求CE的长;
(2)如图2,当P在BC边上运动时,(不与B、C重合)求(AG-CE)/BE 的值;
的值;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com