
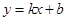 (k>0)和x轴上,已知点B1(1,1),B2(3,2), 则Bn的坐标是_______
(k>0)和x轴上,已知点B1(1,1),B2(3,2), 则Bn的坐标是_______
科目:初中数学 来源:不详 题型:单选题
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 直线 与AB相交于C点,点D从点O出发,以每秒1个单位的速度沿x轴向右运
直线 与AB相交于C点,点D从点O出发,以每秒1个单位的速度沿x轴向右运
 动到点A,过点D作x轴的垂线,分别交直线 和直线 于P,Q两点(P点不与C点重合),以PQ为边向左作正△PQR,设正△PQR与△OBC重叠部分的面积为S(平方单位),点D的运动时间为t(秒)
动到点A,过点D作x轴的垂线,分别交直线 和直线 于P,Q两点(P点不与C点重合),以PQ为边向左作正△PQR,设正△PQR与△OBC重叠部分的面积为S(平方单位),点D的运动时间为t(秒) (1)求点A,B,C的坐标; (2)若点 正好在△PQR的某边上,求t的值;
(1)求点A,B,C的坐标; (2)若点 正好在△PQR的某边上,求t的值; 
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| | 占地面积(m/垄) | 产量(千克/垄) | 利润(元/千克) |
| 西红柿 | 30 | 160 | 1.1 |
| 草莓 | 15 | 50 | 1.6 |
 垄,通过计算说明共有几种种植方案?分别是哪几种?
垄,通过计算说明共有几种种植方案?分别是哪几种?查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com