
【题目】平行四边形ABCD的两个顶点A、C在反比例函数y= ![]() (k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,AD交y轴于P点
(k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,AD交y轴于P点 
(1)已知点A的坐标是(2,3),求k的值及C点的坐标;
(2)若△APO的面积为2,求点D到直线AC的距离.
【答案】
(1)解:∵点A的坐标是(2,3),平行四边形ABCD的两个顶点A、C在反比例函数y= ![]() (k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,
(k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,
∴3= ![]() ,点C与点A关于原点O对称,
,点C与点A关于原点O对称,
∴k=6,C(﹣2,﹣3),
即k的值是6,C点的坐标是(﹣2,﹣3)
(2)解:∵△APO的面积为2,点A的坐标是(2,3),
∴ ![]() ,得OP=2,
,得OP=2,
设过点P(0,2),点A(2,3)的直线解析式为y=ax+b,
![]()
解得, ![]() ,
,
即直线PC的解析式为y= ![]() ,
,
将y=0代入y= ![]() ,得x═﹣4,
,得x═﹣4,
∴OP=4,
∵A(2,3),C(﹣2,﹣3),
∴AC= ![]() ,
,
设点D到AC的距离为m,
∵S△ACD=S△ODA+S△ODC,
∴ ![]() ,
,
解得,m= ![]() ,
,
即点D到直线AC的距离是 ![]()
【解析】(1)根据点A的坐标是(2,3),平行四边形ABCD的两个顶点A、C在反比例函数y= ![]() (k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,可以求得k的值和点C的坐标;(2)根据△APO的面积为2,可以求得OP的长,从而可以求得点P的坐标,进而可以求得直线AP的解析式,从而可以求得点D的坐标,再根据等积法可以求得点D到直线AC的距离.本题考查反比例函数与一次函数的交点问题、平行四边形的性质,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答问题.
(k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,可以求得k的值和点C的坐标;(2)根据△APO的面积为2,可以求得OP的长,从而可以求得点P的坐标,进而可以求得直线AP的解析式,从而可以求得点D的坐标,再根据等积法可以求得点D到直线AC的距离.本题考查反比例函数与一次函数的交点问题、平行四边形的性质,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答问题.
【考点精析】认真审题,首先需要了解平行四边形的性质(平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分).


科目:初中数学 来源: 题型:
【题目】如图,是由两个正方形组成的长方形花坛ABCD,小明从顶点A沿着花坛间小路直到走到长边中点O,再从中点O走到正方形OCDF的中心![]() ,再从中心
,再从中心![]() 走到正方形
走到正方形![]() GFH的中点
GFH的中点![]() ,又从中心
,又从中心![]() 走到正方形
走到正方形![]() IHJ的中心
IHJ的中心![]() ,再从中心
,再从中心![]() 走到正方形
走到正方形![]() KJP的中心
KJP的中心![]() ,一共走了
,一共走了![]() m,则长方形花坛ABCD的周长是( )
m,则长方形花坛ABCD的周长是( )

A. 36m B. 48m C. 96m D. 60m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,∠BAC=60°,△ACD是等边三角形,E是AC的中点,连接BE并延长,交DC于点F,求证: 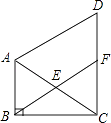
(1)△ABE≌△CFE;
(2)四边形ABFD是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形内,在对角线AC上找到一点P,使PD+PE的和最小,则这个和的最小值是( ).

A. ![]() B.
B. ![]() C. 3 D.
C. 3 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P是△ABC内一点,且它到三角形的三个顶点距离之和最小,则P点叫△ABC的费马点(Fermat point).已经证明:在三个内角均小于120°的△ABC中,当∠APB=∠APC=∠BPC=120°时,P就是△ABC的费马点.若点P是腰长为 ![]() 的等腰直角三角形DEF的费马点,则PD+PE+PF= .
的等腰直角三角形DEF的费马点,则PD+PE+PF= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年5月9日﹣11日,贵州省第十一届旅游产业发展大会在准一市茅台镇举行,大会推出五条遵义精品旅游线路:A红色经典,B醉美丹霞,C生态茶海,D民族风情,E避暑休闲.某校摄影小社团在“祖国好、家乡美”主题宣传周里,随机抽取部分学生举行“最爱旅游路线”投票活动,参与者每人选出一条心中最爱的旅游路线,社团对投票进行了统计,并绘制出如下不完整的条形统计图和扇形统计图,请解决下列问题. 
(1)本次参与投票的总人数是人.
(2)请补全条形统计图.
(3)扇形统计图中,线路D部分的圆心角是度.
(4)全校2400名学生中,请你估计,选择“生态茶海”路线的人数约为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CE=2DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③EG=DE+BG;④AG∥CF;⑤S△FGC=3.6.其中正确结论的个数是( ) 
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为解决都匀市停车难的问题,计划在一段长为56米的路段规划处如图所示的停车位,已知每个车位是长为5米,宽为2米的矩形,且矩形的宽与路的边缘成45°角,则该路段最多可以划出个这样的停车位.(取 ![]() =1.4,结果保留整数)
=1.4,结果保留整数) 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com